JSOI 2016 病毒感染 辅助Dp问题

原题链接：https://www.luogu.com.cn/problem/P5774

分析

　　直接看这道题，第一个困惑点，那个绝对值的比较是什么东西，根据数学知识，我们可以知道这个意思是k到i的距离小于k到j的距离，而路线是线性的，这就意味着当且仅当k在j的左边时才成立，不然总会有k-i>k-j，还不理解？看下图

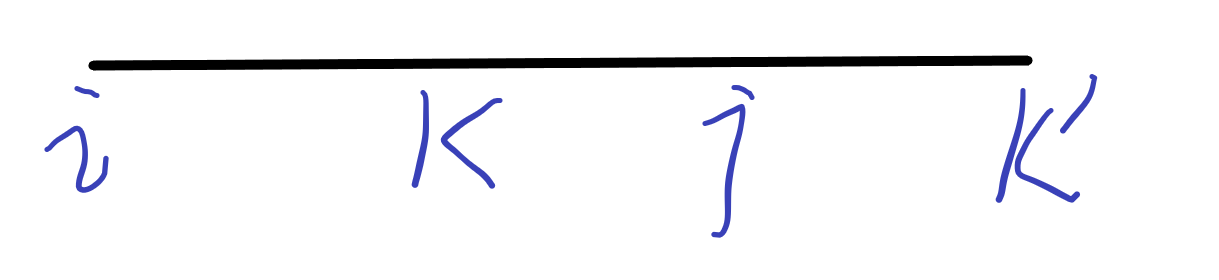
如果K在K'的位置，那么K-i一定大于K-j吧，所以这个题的题意是只要从j往回走去治愈K，就必须把之前没治愈过的村庄也治愈了。

想到这里，状态就差不多出来了，定义DP[i]表示治愈前i个村庄的最小死亡数，下面考虑状态转移，对于JYY来说，每个村庄它都有两个选择，治愈or先去别的再走回来治愈，治愈的话很好弄，主要考虑的就是略过它的情况，这时候如果依次枚举K，效率应该是N^3，程序吃不消，3000的极限数据我们最少也要压到N^2左右，所以接下来考虑优化。

　　优化其实也挺简单的，主要有一点很恶心，下边再说。（从这里开始默认j在i的前边，请勿被上图迷惑）我们发现多出来的时间主要是用在了计算略过村庄再回来的死亡人数的计算，所以我们可以先考虑预处理出从j到i再从i到j然后又回到i这一过程中最少的死亡数，于是定义g[i][j]含义为上述的来辅助我们的DP。我还是补一张图吧……把我自己绕懵了

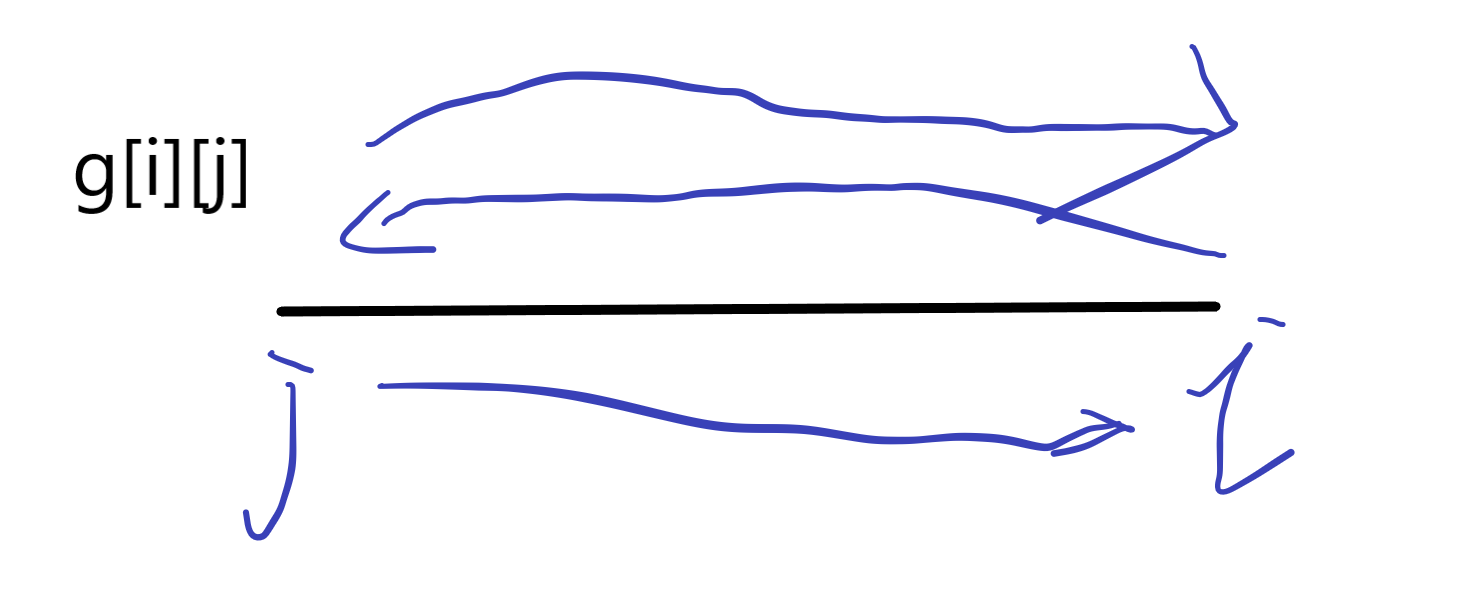
看了这张图我相信你就明白了g数组的含义，接下来考虑如何求解g数组，初始的话g[i][i]肯定是为0的，所以转移都应该从这个位置开始，即倒序，那么怎么转移呢，接下来就是很恶心的一个地方，计算经过的天数！很多题解里都没写到这个，这里详细计算一下。

对于g[i][j]，同样分两种情况讨论，救助或是略过，不管是救助还是略过，都避免不了经过一个区间，就是j+1到i，所以这里可以分而治之，把j和j+1到i这两个分开，g[i][j]的转移中应该需要有g[i][j+1]，这里又启示我们进行倒序循环，同样，不管救助j还是略过，从j走到j+1的这一天里，区间j+1到i这一段的村庄都会死亡（为村民默哀？）所以答案累加Sum（j+1，i）这个可以由前缀和O（1）求出，到了点j+1后，j+1到i的死亡人数就已经被记在了g[i][j+1]里，所以可以不用考虑，这是两种情况所共同具有的死亡人数，下面对两种情况分开讨论，如果救治j的人，那么区间j+1，i的村民就要多死一天，即Sum（j+1，i），不救治呢？因为同样的我们跑路的代价都记录在了g[i][j+1]里边，所以不救治的代价就是在这段时间里j村死亡的人数，你可能问，别的村难道没有死亡的吗？当然可能会有，但我们已经记录了，所以这里不需要再次加入，首先算一下从j跑到i再跑回来所需要的时间，这里举个例子，从4到5要1天，4到6要2天，4到7要3天，所以显然跑路时j村死亡的人是2*（i-j）*a[j]，2是跑了两遍，i-j是刚刚推出来的，a[j]是j村日死亡人数，那只有这些吗？当然不是，这只是跑路的代价，根据定义和题意，j+1到i这些村庄均被治愈且均在略过j后被治愈，所以一个村庄一天，一共就是（i-（j+1）+1）*a[j]天，于是我们的g[i][j]就有了转移方程

　　　　　　　　　　　g[i][j]=g[i][j+1]+Sum（j+1，i）+min（3*（i-j）*a[j]，Sum（j+1，i））

辅助进行转移的方程有了之后我们就可以进行dp的转移了，没错，下边还有很恶心的算时间。

对于每前i个村庄，都不可能直接求出他的最小值，所以要枚举中间点j，即我治愈了前j个村庄，但是j+1被略过了，所以j+1的治愈是从j+1走到i再走回来时才被治愈，这一段的代价就是g[i][j+1]，治愈前j个的代价为dp[j]，直接累加答案即可，那么最硬核的东西就是i+1到n的这段区间，因为在当前阶段，这段区间内的人是不可能被治愈的，所以一天内的死亡人数是Sum（i+1，n），天数呢？根据我之前所推导的，从j+1到i之间反复横跳一来一回一来需要天数3*（i-（j+1）），治愈区间j+1到i需要时间（i-（j+1）+1），这里不要忽略了一个地方，就是从j跑路跑到j+1时还有一天，所以总天数就是3*（i-（j+1））+i-（j+1）+1+1，乘上每天死亡的人数就是最后的代价，累加答案。

至此，这道省选题就落下了帷幕……什么？你问我最后转移的时候没考虑略过i就是一路向右的情况？怎么可能，当我枚举到j=i-1的时候，就相当于转移了这种情况，是吧，所以这个算法是没有问题的，时间复杂度大致为O（n^2）可以A掉

Tips：：如果你实在看不懂时间怎么算的请拿起笔自己模拟一下吧，很快就能懂，我也尽力了。

 #include<iostream>
 #include<cstring>
 #define ll long long
 using namespace std;
 const int N=3e3+;
 ll s[N],g[N][N],dp[N],a[N];
 ll Sum(int l,int r){
     return s[r]-s[l-];
 }
 int main(){
     int n;
     cin>>n;
     for(int i=;i<=n;i++){
         cin>>s[i];a[i]=s[i];s[i]+=s[i-];
     }
     for(int i=;i<=n;i++)
     for(int j=i-;j;j--)
         g[i][j]=g[i][j+]+Sum(j+,i)+min(3LL*(i-j)*a[j],Sum(j+,i));
     memset(dp,0x3f,sizeof dp);
     dp[]=;
     for(int i=;i<=n;i++)
     for(int j=;j<i;j++)
         dp[i]=min(dp[i],dp[j]+g[i][j+]+Sum(i+,n)*((i-(j+))*+i-(j+)+));
     cout<<dp[n];
 }