BZOJ1002 FJOI2007 轮状病毒 【基尔霍夫矩阵+高精度】

BZOJ1002 FJOI2007 轮状病毒

Description

轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的，2个原子之间的边表示这2个原子之间的信息通道。如下图所示

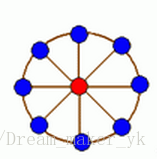
N轮状病毒的产生规律是在一个N轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有16个不同的3轮状病毒，如下图所示



现给定n(N<=100)，编程计算有多少个不同的n轮状病毒

Input

第一行有1个正整数n

Output

计算出的不同的n轮状病毒数输出

Sample Input

3

Sample Output

16

---

基尔霍夫矩阵推一推式子

然后加上高精度

#include<bits/stdc++.h>
using namespace std;
struct Big{
    int t[110],len;
    Big(){len=1;}
};
Big add(Big a,Big b){
    a.len=max(a.len,b.len);
    for(int i=1;i<=a.len;i++)a.t[i]=a.t[i]+b.t[i];
    for(int i=1;i<=a.len;i++){
        if(a.t[i]>=10){
            a.t[i+1]+=a.t[i]/10;
            a.t[i]%=10;
            if(i==a.len)++a.len;
        }
        if(a.t[i]<0){
            a.t[i]+=10;
            a.t[i+1]--;
            if(i+1==a.len&&!a.t[a.len])--a.len;
        }
    }
    return a;
}
Big rdu(Big a,Big b){
    for(int i=1;i<=a.len;i++){
        a.t[i]-=b.t[i];
        if(a.t[i]<0){
            a.t[i]+=10;
            a.t[i+1]--;
        }
    }
    while(!a.t[a.len])a.len--;
    return a;
}
Big add(Big a,int b){
    int tmp=0;
    while(b){
        ++tmp;
        a.t[tmp]+=b;
        b=a.t[tmp]/10;
        a.t[tmp]%=10;
    }
    a.len=max(a.len,tmp);
    return a;
}
Big mul(Big a,int b){
    for(int i=1;i<=a.len;i++)a.t[i]*=b;
    for(int i=1;i<=a.len;i++){
        if(a.t[i]>=10){
            a.t[i+1]+=a.t[i]/10;
            a.t[i]%=10;
            if(i==a.len)++a.len;
        }
    }
    return a;
}
Big f[101];
int main(){
    f[1].t[1]=1;
    f[2].t[1]=5;
    int n;cin>>n;
    for(int i=3;i<=n;i++)f[i]=add(rdu(mul(f[i-1],3),f[i-2]),2);
    for(int i=f[n].len;i>=1;i--)printf("%d",f[n].t[i]);
    return 0;
}