Uva1343-The Rotation Game-IDA*算法

原题https://uva.onlinejudge.org/external/13/1343.pdf

---

题意：　　

有个＃字型的棋盘，2行2列，一共24个格。

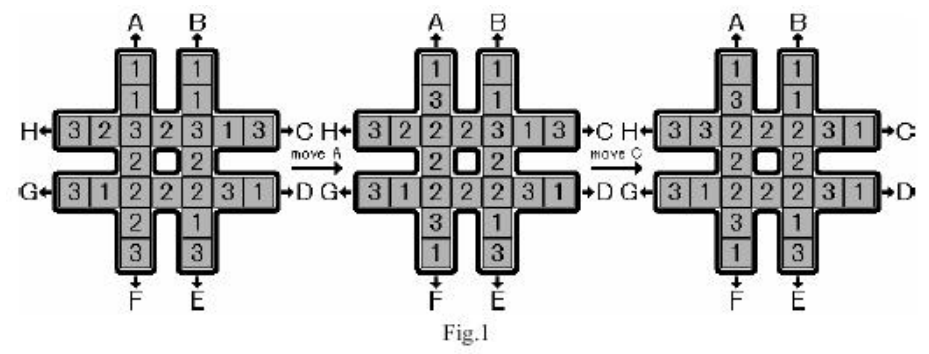
如图：每个格子是1或2或3，一共8个1，8个2，8个3.

有A~H一共8种合法操作，比如A代表把A这一列向上移动一个，最上面的格会补到最下面。

求：使中心8个格子数字一致的最少步骤，要输出具体的操作步骤及最终中心区域的数字。如果有多个解，输出字典序最小的操作步骤。

---

分析：

很明显的一个状态空间搜索问题，不过可以注意到，虽然每一个状态有八个可能的后续状态，随着操作数n的增加，总状态数 8^n 还是大得可怕。比如当n＝11时，总状态为8^11 = 85亿。就算通过自己创建特制的哈希表进行状态判重，优化效果并不明显，因为最近一直在做状态空间搜索问题，即使用bfs＋剪枝＋哈希表，这些程序都无一例外的超时了，所以现在看到状态空间搜索问题，如果没有特别好的剪枝，我绝对不敢用bfs了.....

回到这道题，所有可以用bfs,回溯解决的问题，尤其是解答树的结点数没有明显上限的题，选择用迭代加深搜索算法都特别好用（原因可以参考我上一篇文章）。这里IDA*(迭代加深A*算法)其实说白了就是迭代加深+剪枝.

A*算法是对于每一步考虑 g(n) + h()和MAXD的关系。

稍微解释一下，g(n)是从起点到当前状态的总步数，MAXD是我们提前通过计算证明得到的最短路线总步数的上限，h()是启发函数，是整个算法的关键，我们设计的h()可以预估从当前状态到目标状态至少需要的步数。

这样，上面的关系式就很好理解了。g(n) + h() > MAXD 意味着当前已经走的步数＋至少还需要的步数 > 我可以走的步数上限，这种状态，必然已经没有继续的必要，回溯。

对于这道题，可以注意到，对于每一次操作，我们最多可以让中心格子多一个目标数字，如果当前中心格子待整理的数字个数大于我们还可以走的步数，回溯。

这样，就得到了

　　　　if (d + num_unordered() > MAXD) return false;

　　　　这一核心剪枝公式。 剩下的就简单了。

代码只有52行，还是很简洁的。而且运行速度很快。过30组数据只用了126ms.

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 const int MAXN = , LEN = ;
 int board[LEN][LEN - ] = { {, , , , , , }, {, , , , , , },
                         {, , , , , , }, {, , , , , , },
                         {, , , , , , }, {, , , , , , },
                         {, , , , , , }, {, , , , , , } };
 int check_order[] = {, , , , , , , }, a[MAXN], maxd;
 char order[];

 int unordered() {
     int n1 = , n2 = , n3 = ;
     for (int i = ; i < LEN; i++)
         if (a[check_order[i]] == )  n1++;
         else if (a[check_order[i]] == ) n2++;
         else n3++;
     return LEN - max(max(n1, n2), n3);
 }

 void rotate(int di) {
     int t = a[board[di][]];
     for (int i = ; i < LEN - ; i++) a[board[di][i - ]] = a[board[di][i]];
     a[board[di][LEN - ]] = t;
 }

 bool dfs(int d) {
     int cnt = unordered();
     if (!cnt) return true;
     if (cnt + d > maxd) return false;
     int temp[MAXN]; memcpy(temp, a, sizeof(a));
     for (int i = ; i < LEN; i++) {
         rotate(i);
         order[d] = i + 'A';
         if (dfs(d + )) return true;
         memcpy(a, temp, sizeof(a));
     }
     return false;
 }

 int main() {
     freopen("in", "r", stdin);
     while (scanf("%d", &a[]) && a[]) {
         for (int i = ; i < MAXN; i++) scanf("%d", &a[i]);
         if (!unordered()) { printf("No moves needed\n%d\n", a[]); continue;}
         for (maxd = ;; maxd++) if (dfs()) break;
         for (int i = ; i < maxd; i++) printf("%c", order[i]);
         printf("\n%d\n", a[]);
     }
     return ;
 }

顺便纪念一下排第六（前面3个是virtual oj......）