【pytorch学习】之微积分

4 微积分

在2500年前，古希腊人把一个多边形分成三角形，并把它们的面积相加，才找到计算多边形面积的方法。为了求出曲线形状（比如圆）的面积，古希腊人在这样的形状上刻内接多边形。如图所示，内接多边形的等长边越多，就越接近圆。这个过程也被称为逼近法（method of exhaustion）

事实上，逼近法就是积分（integral calculus）的起源。2000多年后，微积分的另一支，微分（differentialcalculus）被发明出来。在微分学最重要的应用是优化问题，即考虑如何把事情做到最好。这种问题在深度学习中是无处不在的。在深度学习中，我们“训练”模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。通常情况下，变得更好意味着最小化一个损失函数（loss function），即一个衡量“模型有多糟糕”这个问题的分数。最终，我们真正关心的是生成一个模型，它能够在从未见过的数据上表现良好。但“训练”模型只能将模型与我们实际能看到的数据相拟合。因此，我们可以将拟合模型的任务分解为两个关键问题：

• 优化（optimization）：用模型拟合观测数据的过程；
• 泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

4.1 导数和微分

我们首先讨论导数的计算，这是几乎所有深度学习优化算法的关键步骤。在深度学习中，我们通常选择对于模型参数可微的损失函数。简而言之，对于每个参数，如果我们把这个参数增加或减少一个无穷小的量，可以知道损失会以多快的速度增加或减少，假设我们有一个函数\(f : \mathbb{R} \rightarrow \mathbb{R}\) ，其输入和输出都是标量。如果f的导数存在，这个极限被定义为

\[f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}
\]

如果f在一个区间内的每个数上都是可微的，则此函数在此区间中是可微。如果f′(a)存在，则称f在a处是可微（differentiable）的。

我们可以将导数f′(x)解释为f(x)相对于x的瞬时（instantaneous）变化率。所谓的瞬时变化率是基于x中的变化h，且h接近0。为了更好地解释导数，让我们做一个实验。

%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
def f(x):
    return 3 * x ** 2 - 4 * x

当x = 1时，导数u′是2。

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h
h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1

h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

为了对导数的这种解释进行可视化，我们将使用matplotlib，这是一个Python中流行的绘图库。要配

置matplotlib生成图形的属性，我们需要定义几个函数。在下面，use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像。

def use_svg_display(): #@save

    backend_inline.set_matplotlib_formats('svg')

我们定义set_figsize函数来设置图表大小。因为导入语句 from matplotlib mport pyplot as plt已标记为保存中。

def set_figsize(figsize=(3.5, 2.5)): #@save
    """设置matplotlib的图表大小"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

下面的set_axes函数用于设置由matplotlib生成图表的轴的属性。

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

通过这三个用于图形配置的函数，定义一个plot函数来简洁地绘制多条曲线。

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,ylim=None, xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点"""
    if legend is None:
        legend = []
    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()
    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)and not hasattr(X[0], "__len__"))
    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

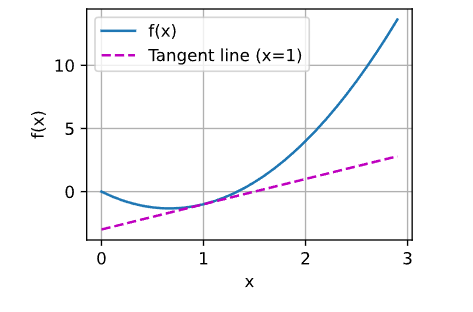
现在我们可以绘制函数u = f(x)及其在x = 1处的切线y = 2x − 3，其中系数2是切线的斜率。

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

4.2 偏导数

到目前为止，我们只讨论了仅含一个变量的函数的微分。在深度学习中，函数通常依赖于许多变量。因此，我们需要将微分的思想推广到多元函数（multivariate function）上。

设\(y = f(x_1, x_2, . . . , x_n)\)是一个具有n个变量的函数。\(y\)关于第\(i\)个参数\(x_i\)的偏导数（partial derivative）为：

\[\frac{\partial f}{\partial x_i} = \lim_{{h \to 0}} \frac{f(x_1, \ldots, x_{i-1}, x_i + h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}
\]

4.3 梯度

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。具体而言，设

函数\(f: \mathbb{R}^n \rightarrow \mathbb{R}\)的输入是一个n维向量\(\mathbf{x} = [x_1, x_2, \ldots, x_n]^T\)，并且输出是一个标量。函数f(x)相对于x的梯度是一个包含n个偏导数的向量:

\[\nabla f(\mathbf{x}) = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right]^T
\]

4.4 链式法则

然而，上面方法可能很难找到梯度。这是因为在深度学习中，多元函数通常是复合（composite）的，所以难以应用上述任何规则来微分这些函数。幸运的是，链式法则可以被用来微分复合函数。

让我们先考虑单变量函数。假设函数y = f(u)和u = g(x)都是可微的，根据链式法则：

\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}
\]

现在考虑一个更一般的场景，即函数具有任意数量的变量的情况。假设可微分函数y有变量 $( x_1, x_2, \ldots, x_n ) $，其中每个可微分函数 \(u_i\) 都有变量 \(( u_1, u_2, \ldots, u_m )\)。注意，y是 $( x_1, x_2, \ldots, x_n ) $的函数。链式法则给出：

\[\frac{{\partial y}}{{\partial x_i}} = \sum_{j=1}^{m} \frac{{\partial y}}{{\partial u_j}} \cdot \frac{{\partial u_j}}{{\partial x_i}}
\]

声明：

本系列学习笔记主要以《动手学深度学习》的pytorch版本为主。

详细见GitHub：https://github.com/d2l-ai/d2l-zh

或者 https://zh.d2l.ai/