C++复数四则运算的实现

程序主要实现复数的加减乘，数乘，取共轭功能。

将所有函数都定义为了成员函数。

使用库函数atof将字符串转换为浮点型数据。

函数主要难点在于处理输入。由于需要判断输入是选择退出还是继续，所以用字符串来接收输入，判断是否为q或Q后将字符串转换为double型。

由于库函数中定义了complex类，因此，这里的类名改为comple。

类声明

#ifndef  COMPLEX_H_
#define  COMPLEX_H_

#include<iostream>
using namespace std;

class comple
{
    private:
        double re;
        double im;
    public:
        comple(double r=0.0, double i=0.0);
        ~comple();
        comple operator+(const comple & a) const;
        comple operator-(const comple & a) const;
        comple operator*(const comple & a) const;
        comple operator~() const;
        comple operator*(const double x) const;
        friend ostream & operator<<(ostream & os, const comple & b);
        friend int operator>>(istream & is, comple & b);
        friend comple operator*(const double x, const comple & b);

};

#endif

方法定义

#include"complex0.h"
#include<iostream>
#include<math.h> //strlen函数头文件
#include"string.h"
#include<cstdlib>//atof函数头文件
using namespace std;

comple::comple(double r, double i)
{
    re=r;
    im=i;
}

comple::~comple()
{

}

comple comple::operator+(const comple & a) const
{
    comple temp;
    temp.re=re+a.re;
    temp.im=im+a.im;
    return temp;
}

comple comple::operator-(const comple & a) const
{
    comple temp;
    temp.re=re-a.re;
    temp.im=im-a.im;
    return temp;
}

comple comple::operator*(const comple & a) const
{
    comple temp;
    temp.re=re*a.re-im*a.im;
    temp.im=re*a.im+im*a.re;
    return temp;
}

comple comple::operator~() const
{
    comple temp;
    temp.re=re;
    temp.im=-im;
    return temp;
}

comple comple::operator*(const double x ) const
{
    return comple(x*re,x*im);
}

ostream & operator<<(ostream & os, const comple & b)
{
    os << "(" <<b.re <<"," <<b.im << "i)";
    return os;
}

int operator>>(istream & is, comple & b)
{
    double c1,c2;
    char s[],*str;
    int c,i;
    cout << "real:";
    is >> s;
    c=strlen(s);
    str=s;
    for(i=;i<c;i++)
     if(s[i]=='q'||s[i]=='Q')
     return ;

    if((s[]>'')&&(s[]<''))
    c1=atof(str);

    cout << "imaginary:";
    is >> s;
    c=strlen(s);
    str=s;
    for(i=;i<c;i++)
    {
     if(s[i]=='q'||s[i]=='Q')
     return ;
    }

    if(s[]>''&&s[]<'')
    c2=atof(str);

    b=comple(c1,c2);
    return ;

}

comple operator*(double x, const comple & b)
{
    return b*x;
}

测试程序

#include<iostream>
#include"complex0.h"

using namespace std;

int main()
{
    comple a(3.0,4.0);
    comple c;

    cout << "Enter a complex number (q to quit):\n";
    while(cin >> c)
    {
        cout << "c is " << c << endl;
        cout << "complex conjugate is " << ~c <<endl;
        cout << "a is " << a << endl;
        cout << "a+c is " << a+c << endl;
        cout << "a-c is " << a-c << endl;
        cout << "a*c is " << a*c << endl;
        cout << "2*c is " << *c << endl;
        cout << "Enter a complex number (q to quit):\n";
    }
    cout << "Done!\n";
    return ;
}

测试结果

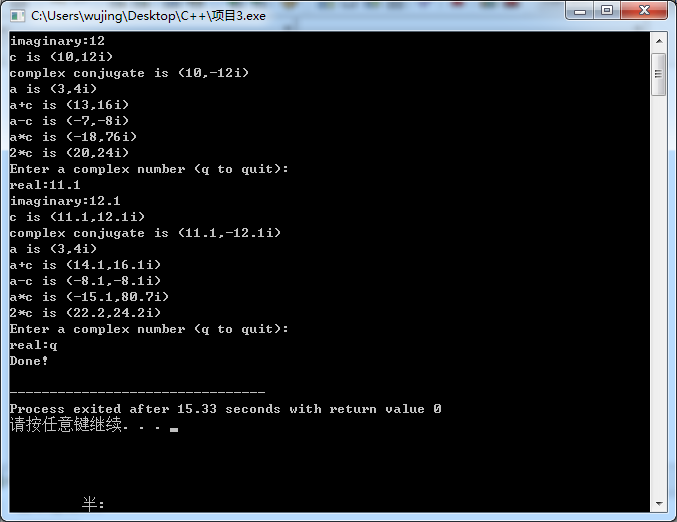
atof函数补充

包含的头文件在c中为#include<stdlib.h>，c++中为include<cstdlib>

http://www.cppblog.com/cxiaojia/archive/2012/02/24/166436.html

http://my.oschina.net/Tsybius2014/blog/338234

http://www.cnblogs.com/lidabo/archive/2012/07/10/2584706.html

http://blog.csdn.net/cxh342968816/article/details/6627768

标准c++库函数中复数四则运算程序

#ifndef __MYCOMPLEX__
#define __MYCOMPLEX__

class complex;
complex&
  __doapl (complex* ths, const complex& r);
complex&
  __doami (complex* ths, const complex& r);
complex&
  __doaml (complex* ths, const complex& r);

class complex
{
public:
  complex (double r = , double i = ): re (r), im (i) { }
  complex& operator += (const complex&);
  complex& operator -= (const complex&);
  complex& operator *= (const complex&);
  complex& operator /= (const complex&);
  double real () const { return re; }
  double imag () const { return im; }
private:
  double re, im;

  friend complex& __doapl (complex *, const complex&);
  friend complex& __doami (complex *, const complex&);
  friend complex& __doaml (complex *, const complex&);
};

inline complex&
__doapl (complex* ths, const complex& r)
{
  ths->re += r.re;
  ths->im += r.im;
  return *ths;
}

inline complex&
complex::operator += (const complex& r)
{
  return __doapl (this, r);
}

inline complex&
__doami (complex* ths, const complex& r)
{
  ths->re -= r.re;
  ths->im -= r.im;
  return *ths;
}

inline complex&
complex::operator -= (const complex& r)
{
  return __doami (this, r);
}

inline complex&
__doaml (complex* ths, const complex& r)
{
  double f = ths->re * r.re - ths->im * r.im;
  ths->im = ths->re * r.im + ths->im * r.re;
  ths->re = f;
  return *ths;
}

inline complex&
complex::operator *= (const complex& r)
{
  return __doaml (this, r);
}

inline double
imag (const complex& x)
{
  return x.imag ();
}

inline double
real (const complex& x)
{
  return x.real ();
}

inline complex
operator + (const complex& x, const complex& y)
{
  return complex (real (x) + real (y), imag (x) + imag (y));
}

inline complex
operator + (const complex& x, double y)
{
  return complex (real (x) + y, imag (x));
}

inline complex
operator + (double x, const complex& y)
{
  return complex (x + real (y), imag (y));
}

inline complex
operator - (const complex& x, const complex& y)
{
  return complex (real (x) - real (y), imag (x) - imag (y));
}

inline complex
operator - (const complex& x, double y)
{
  return complex (real (x) - y, imag (x));
}

inline complex
operator - (double x, const complex& y)
{
  return complex (x - real (y), - imag (y));
}

inline complex
operator * (const complex& x, const complex& y)
{
  return complex (real (x) * real (y) - imag (x) * imag (y),
               real (x) * imag (y) + imag (x) * real (y));
}

inline complex
operator * (const complex& x, double y)
{
  return complex (real (x) * y, imag (x) * y);
}

inline complex
operator * (double x, const complex& y)
{
  return complex (x * real (y), x * imag (y));
}

complex
operator / (const complex& x, double y)
{
  return complex (real (x) / y, imag (x) / y);
}

inline complex
operator + (const complex& x)
{
  return x;
}

inline complex
operator - (const complex& x)
{
  return complex (-real (x), -imag (x));
}

inline bool
operator == (const complex& x, const complex& y)
{
  return real (x) == real (y) && imag (x) == imag (y);
}

inline bool
operator == (const complex& x, double y)
{
  return real (x) == y && imag (x) == ;
}

inline bool
operator == (double x, const complex& y)
{
  return x == real (y) && imag (y) == ;
}

inline bool
operator != (const complex& x, const complex& y)
{
  return real (x) != real (y) || imag (x) != imag (y);
}

inline bool
operator != (const complex& x, double y)
{
  return real (x) != y || imag (x) != ;
}

inline bool
operator != (double x, const complex& y)
{
  return x != real (y) || imag (y) != ;
}

#include <cmath>

inline complex
polar (double r, double t)
{
  return complex (r * cos (t), r * sin (t));
}

inline complex
conj (const complex& x)
{
  return complex (real (x), -imag (x));
}

inline double
norm (const complex& x)
{
  return real (x) * real (x) + imag (x) * imag (x);
}

#endif   //__MYCOMPLEX__

测试程序

#include <iostream>
#include "complex.h"

using namespace std;

ostream&
operator << (ostream& os, const complex& x)
{
  return os << '(' << real (x) << ',' << imag (x) << ')';
}

int main()
{
  complex c1(, );
  complex c2(, );

  cout << c1 << endl;
  cout << c2 << endl;

  cout << c1+c2 << endl;
  cout << c1-c2 << endl;
  cout << c1*c2 << endl;
  cout << c1 /  << endl;

  cout << conj(c1) << endl;
  cout << norm(c1) << endl;
  cout << polar(,) << endl;

  cout << (c1 += c2) << endl;

  cout << (c1 == c2) << endl;
  cout << (c1 != c2) << endl;
  cout << +c2 << endl;
  cout << -c2 << endl;

  cout << (c2 - ) << endl;
  cout << ( + c2) << endl;

  return ;
}