Ex3_2 最近点对

原文链接http://blog.csdn.net/zyang008/article/details/6175587

分治法

1）算法描述：已知集合S中有n个点，分治法的思想就是将S进行拆分，分为2部分求最近点对。算法每次选择一条垂线L，将S拆分左右两部分为S_L和S_R，L一般取点集S中所有点的中间点的x坐标来划分，这样可以保证S_L和S_R中的点数目各为n/2，

（否则以其他方式划分S，有可能导致S_L和S_R中点数目一个为1，一个为n-1，不利于算法效率，要尽量保持树的平衡性）

依次找出这两部分中的最小点对距离：δ_L和δ_R，记S_L和S_R中最小点对距离δ = min（δ_L，δ_R），如图1：

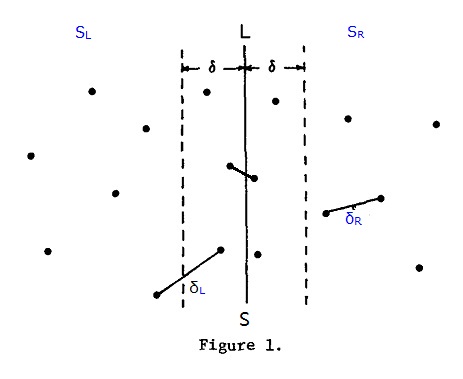
以L为中心，δ为半径划分一个长带，最小点对还有可能存在于S_L和S_R的交界处，如下图2左图中的虚线带，p点和q点分别位于S_L和S_R的虚线范围内，在这个范围内，p点和q点之间的距离才会小于δ，最小点对计算才有意义。

Figure 2

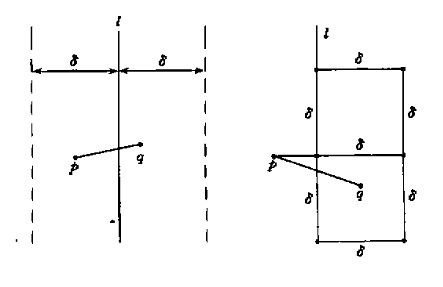
对于S_L虚框范围内的p点，在S_R虚框中与p点距离小于δ的顶多只有六个点，就是图二右图中的2个正方形的6的顶点。这个可以反推证明，如果右边这2个正方形内有7个点与p点距离小于δ，例如q点，则q点与下面正方形的四个顶点距离小于δ，则和δ为S_L和S_R中的最小点对距离相矛盾。因此对于S_L虚框中的p点，不需求出p点和右边虚线框内所有点距离，只需计算S_R中与p点y坐标距离最近的6个点，就可以求出最近点对，节省了比较次数。

（否则的话，最坏情形下，在S_R虚框中有可能会有n/2个点，对于S_L虚框中的p点，每次要比较n/2次，浪费了算法的效率）

代码描述：

1）对点集S的点x坐标和y坐标进行升序排序，获得点集S_x和S_y

2）令δ=∞;   //δ为最小点位距离

3）Divide_conquer（S_x，S_y，δ）  //分治法

if （S_x.count=1） then δ=∞;    //如果S_x中只有一个点，则δ=∞

return δ;

else if（S_x.count=2 and d（S_x.[0],S_x.[1]）<δ） //如果S_x中只有2个点，则δ为两点之间距离

δ=d（S_x.[0],）S_x.[1]）;

return δ;

else    //如果S_x中多于2个点，则将S_x,S_y分治，以中心点画线，将S_x分为左右两部分S_xL和S_xR，S_y分为S_yL和S_yR

j₁=1,j₂=1,k₁=1,k₂=1;

mid = S_x.count/2;   //mid为S_x中的中间点点号

L = S_x.[mid].x;      //L为S_x中的中间点x坐标

for(i=1,i<S_x.count,i++)

{

if(i<=mid)     //将S_x中间线以左地方的点存入到S_xL，新数组保持原来的升序性质

S_xL[k₁] = S_x[i]   k₁++;

else   //将S_x中间线以右的地方的点存入到S_xR，新数组保持原来的升序性质

S_xR.count[k₂] = S_x[i]   k₂++;

if(S_y[i].x <L)   //将S_y中间线以左地方的点存入到S_yL，新数组保持原来的升序性质

S_yL[j₁] = S_x[i]   j₁++;

else   //将S_y中间线以右地方的点存入到S_yR，新数组保持原来的升序性质

S_yR[j₂] = S_x[i]   j₂++;

}

δ_L = Divide_conquer（S_xL，S_yL，δ）;    //获取S_x中的的最小点位距离δ_L

δ_R = Divide_conquer（S_xR，S_yR，δ）;   //获取S_y中的的最小点位距离δ_R

δ= min (δ_L,δ_R);

δ=merge(S_yL，S_yR，δ);    //获S_x中S_y交界处的最小点位距离，并综合 δ_L和δ_R 求出点集的最小点位距离δ

return δ;

函数merge(S_yL，S_yR，δ)

merge(S_yL，S_yR，δ)

{

i₁=1,i₂=1;

for(i=1,i<S_yL.count,i++)   //获取S_yL中在左边虚框(距离小于δ)内的点，存入到S'_yL中，新数组保持原来的升序性质

{

if(S_yL[i].x>L-δ)

then S'_yL[i₁]= S_yL[i], i₁++,

}

for(i=1,i<S_yR.count,i++)  //获取S_yR中在右边虚框(距离小于δ)内的点，存入到S'_yR中，新数组保持原来的升序性质

{

if(S_yR[i].x<L+δ)

then S'_yR[i₂]= S_yR[i], i₂++,

}

t=1;

for(i=1,i<S'_yL.count,i++)

{

while(S'_yR[t].y< S'_yL[t].y and t < S_yR.count)  //获取点集S'_yR内距离点S'_yL[t]y坐标最接近的点号

{ t++; }

for( j= max(1,t-3), j<=min(t+3,S'_yR.count),j++)   //计算S'_yR中的点与S'_yL[t]y坐标相邻的六个点的距离

{

if(d(S'_yL[i],S'_yL[j])<δ)    //如果前两点之间距离小于δ

then δ = d(S'_yL[i],S'_yL[j]);   //则最小点位距离δ为当前两点之间距离

}

return δ

}

3）算法时间复杂度：

首先对点集S的点x坐标和y坐标进行升序排序，需要循环2nlogn次，复杂度为O(2nlogn)

接下来在分治过程中，对于每个S'_yL中的点，都需要与S'_yR中的6个点进行比较

O(n)= 2O(n/2) + (n/2)*6  （一个点集划分为左右两个点集，时间复杂度为左右两个点集加上中间区域运算之和）

其解为O(n)< O(3nlogn)

因此总的时间复杂度为O(3nlogn)，比蛮力法的O(n²)要高效。