目录

　　一维Full卷积

　　一维Same卷积

　　一维Valid卷积

　　三种卷积类型的关系

　　具备深度的一维卷积

　　具备深度的张量与多个卷积核的卷积

　　参考资料

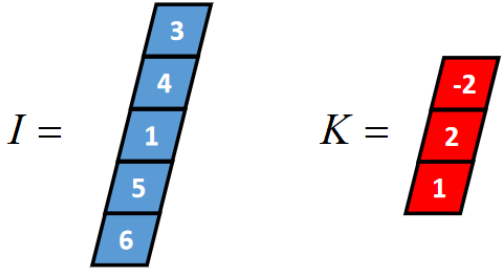
一维卷积通常有三种类型：full卷积、same卷积和valid卷积，下面以一个长度为5的一维张量I和长度为3的一维张量K（卷积核）为例，介绍这三种卷积的计算过程

一维Full卷积

Full卷积的计算过程是：K沿着I顺序移动，每移动到一个固定位置，对应位置的值相乘再求和，计算过程如下：

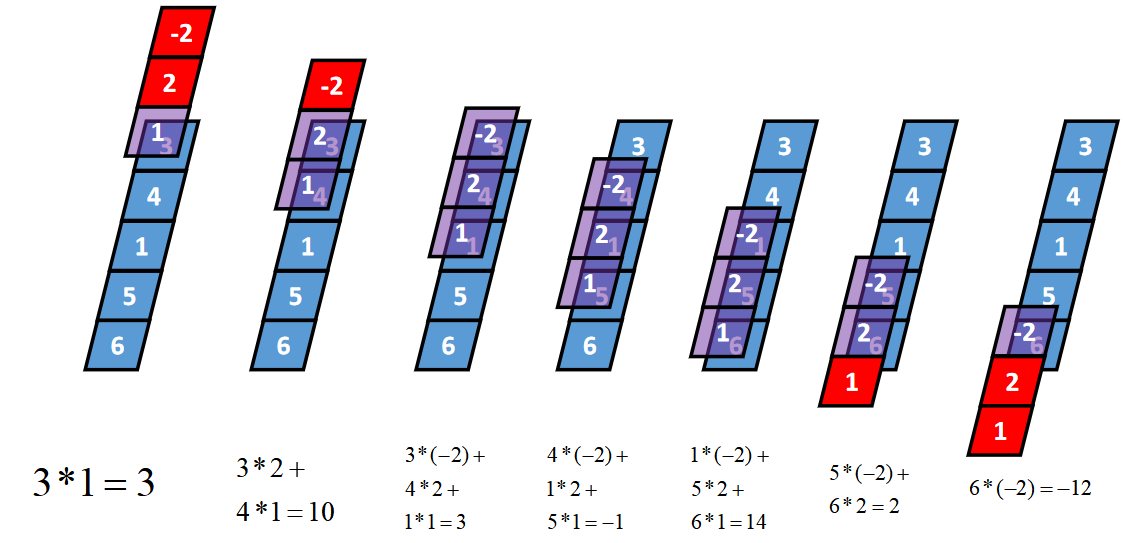
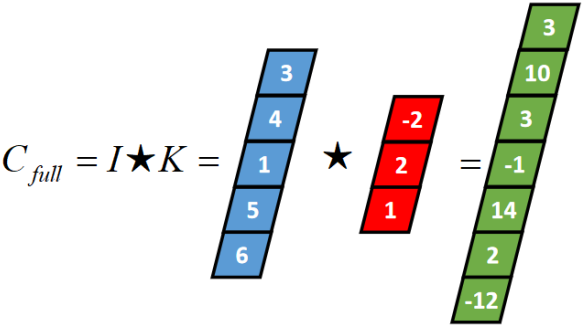
将得到的值依次存入一维张量Cfull，该张量就是I和卷积核K的full卷积结果，其中K卷积核或者滤波器或者卷积掩码，卷积符号用符号★表示，记Cfull=I★K

返回目录

一维Same卷积

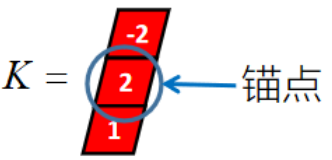
卷积核K都有一个锚点，然后将锚点顺序移动到张量I的每一个位置处，对应位置相乘再求和，计算过程如下：

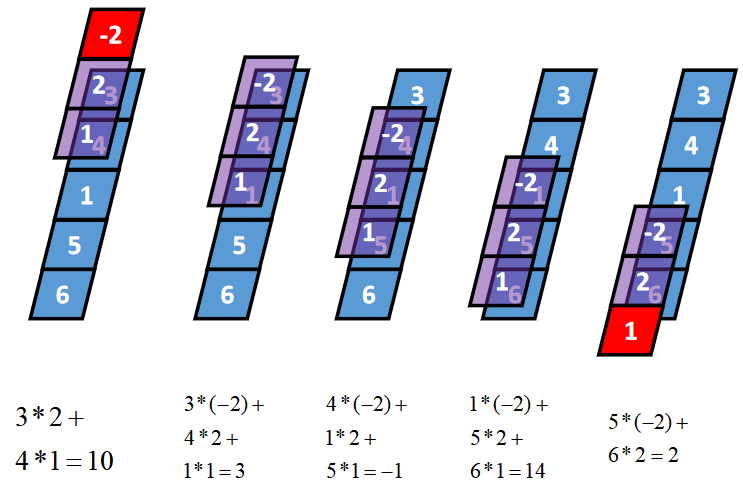
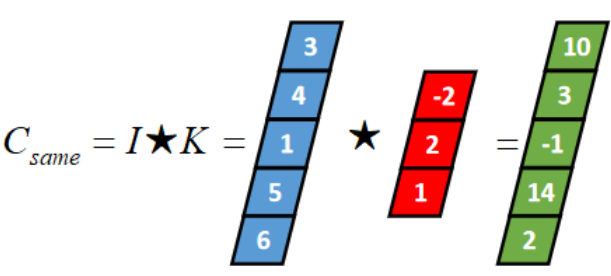
假设卷积核的长度为FL，如果FL为奇数，锚点位置在(FL-1)/2处；如果FL为偶数，锚点位置在(FL-2)/2处。

返回目录

一维Valid卷积

从full卷积的计算过程可知，如果K靠近I，就会有部分延伸到I之外，valid卷积只考虑I能完全覆盖K的情况，即K在I的内部移动的情况，计算过程如下：

返回目录

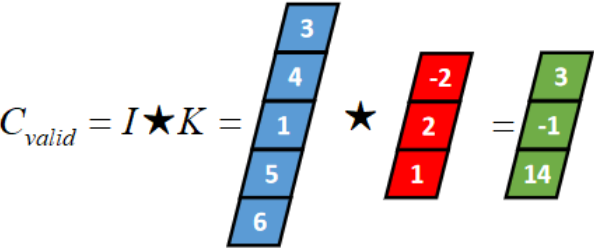
三种卷积类型的关系

返回目录

具备深度的一维卷积

比如x是一个长度为3，深度为3的张量，其same卷积过程如下，卷积核K的锚点在张量x范围内依次移动，输入张量的深度和卷积核的深度是相等的。

返回目录

具备深度的张量与多个卷积核的卷积

上面介绍了一个张量和一个卷积核进行卷积。他们的深度相等才能进行卷积，下面介绍一个张量与多个卷积核的卷积。同一个张量与多个卷积核的卷积本质上是该张量分别与每一个卷积核卷积，然后将每一个卷积结果在深度方向上连接起来。

举例：以长度为3、深度为3的输入张量与2个长度为2、深度为3的卷积核卷积为例，过程如下：

返回目录

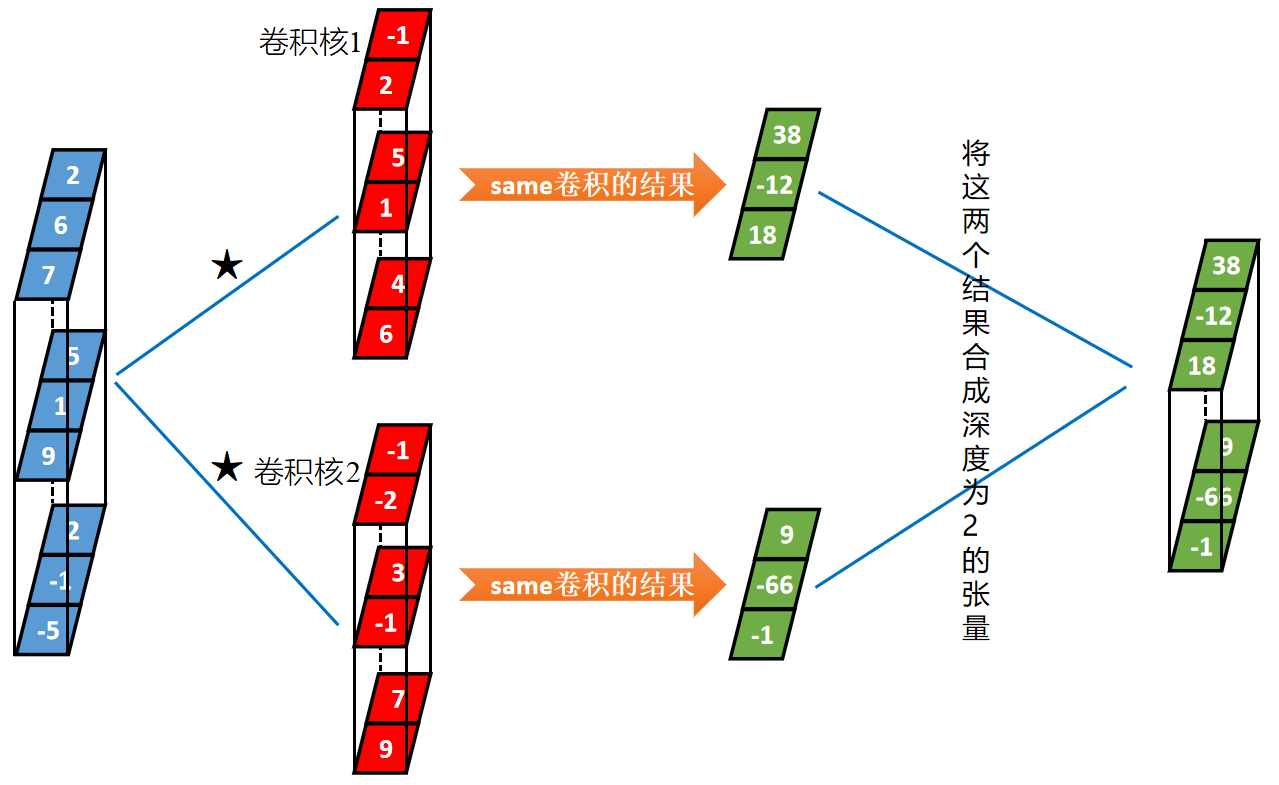
参考资料

《图解深度学习与神经网络：从张量到TensorFlow实现》_张平

返回目录

深度学习面试题09：一维卷积（Full卷积、Same卷积、Valid卷积、带深度的一维卷积）的更多相关文章

  1. 深度学习面试题27：非对称卷积(Asymmetric Convolutions)

    目录 产生背景 举例 参考资料 产生背景 之前在深度学习面试题16:小卷积核级联卷积VS大卷积核卷积中介绍过小卷积核的三个优势: ①整合了三个非线性激活层,代替单一非线性激活层,增加了判别能力. ②减 ...

  2. 深度学习面试题29：GoogLeNet(Inception V3)

    目录 使用非对称卷积分解大filters 重新设计pooling层 辅助构造器 使用标签平滑 参考资料 在<深度学习面试题20:GoogLeNet(Inception V1)>和<深 ...

  3. 深度学习面试题13：AlexNet(1000类图像分类)

    目录 网络结构 两大创新点 参考资料 第一个典型的CNN是LeNet5网络结构,但是第一个引起大家注意的网络却是AlexNet,Alex Krizhevsky其实是Hinton的学生,这个团队领导者是 ...

  4. 深度学习面试题10：二维卷积（Full卷积、Same卷积、Valid卷积、带深度的二维卷积）

    目录 二维Full卷积 二维Same卷积 二维Valid卷积 三种卷积类型的关系 具备深度的二维卷积 具备深度的张量与多个卷积核的卷积 参考资料 二维卷积的原理和一维卷积类似,也有full卷积.sam ...

  5. 深度学习面试题25：分离卷积(separable卷积)

    目录 举例 单个张量与多个卷积核的分离卷积 参考资料 举例 分离卷积就是先在深度上分别卷积,然后再进行卷积,对应代码为: import tensorflow as tf # [batch, in_he ...

  6. 深度学习面试题24：在每个深度上分别卷积(depthwise卷积)

    目录 举例 单个张量与多个卷积核在深度上分别卷积 参考资料 举例 如下张量x和卷积核K进行depthwise_conv2d卷积 结果为: depthwise_conv2d和conv2d的不同之处在于c ...

  7. 深度学习面试题16：小卷积核级联卷积VS大卷积核卷积

    目录 感受野 多个小卷积核连续卷积和单个大卷积核卷积的作用相同 小卷积核的优势 参考资料 感受野 在卷积神经网络中,感受野(Receptive Field)的定义是卷积神经网络每一层输出的特征图(fe ...

  8. 深度学习面试题26：GoogLeNet(Inception V2)

    目录 第一层卷积换为分离卷积 一些层的卷积核的个数发生了变化 多个小卷积核代替大卷积核 一些最大值池化换为了平均值池化 完整代码 参考资料 第一层卷积换为分离卷积 net = slim.separab ...

  9. 深度学习面试题21：批量归一化(Batch Normalization,BN)

    目录 BN的由来 BN的作用 BN的操作阶段 BN的操作流程 BN可以防止梯度消失吗 为什么归一化后还要放缩和平移 BN在GoogLeNet中的应用 参考资料 BN的由来 BN是由Google于201 ...

随机推荐

  1. 蓝牙 BLE 三种 UUID 格式转换

    蓝牙广播中对服务 UUID 格式定义都有三种 16 bit UUID.32 bit UUID.128 bit UUID. 但是熟悉安卓开发的小伙伴都知道接口都 UUID 格式,fromString 时 ...

  2. iOS进阶之多线程--NSThread详解

    NSThread简介 NSThread是苹果官方提供面向对象操作线程的技术,简单方便,可以直接操作线程对象,不过需要自己控制线程的生命周期.在平时使用很少,最常用到的无非就是 [NSThread cu ...

  3. 【转】MCU厂商简介

    国内MCU市场已达360亿元,2020年将超500亿元.2016年,国内MCU市场已达360亿元,同比增长达11%,而据IC Insights预测,随着中国大陆汽车电子和物联网领域的快速发展,对MCU ...

  4. Docker——概念学习

    百度百科概念: Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Linux或Windows 机器上,也可以实现虚拟化.容器是完全 ...

  5. JAVA对象结构

    对象的内存布局 在HotSpot虚拟机中,对象在内存中存储的布局可以分为3块区域:对象头(Header),实例数据(Instance Data)和对象填充(Padding). 实例数据:对象真正存储的 ...

  6. jupytext library using in jupyter notebook

    目录 1. jupytext features 2. Way of using 3. usage 4. installation 1. jupytext features Jupytext can s ...

  7. 0032ActiveMQ之java编码实现生产者和消费者操作队列queue

    今天学习了入门级的用java编写生产者producer和消费者consumer操作activemq的queue队列,为了之后复习回顾,现做整理如下: maven工程的搭建此处不再讲解,在maven工程 ...

  8. LINUX系统的常用知识

    常用的命令: man config   查看linux里面所有命令的详细描述 man pwd   按回车是一行一行的走,按空格是一页一页的走,按q键是退出的意思 mkdir test   创建文件夹p ...

  9. 置换及Pólya定理

    听大佬们说了这么久Pólya定理,终于有时间把这个定理学习一下了. 置换(permutation)简单来说就是一个(全)排列,比如 \(1,2,3,4\) 的一个置换为 \(3,1,2,4\).一般地 ...

  10. 两点三次Hermiter插值C++代码

    #include <math.h> #include <gl/glut.h> #include <iostream> using namespace std; st ...