【xsy1611】 数位dp 数位dp

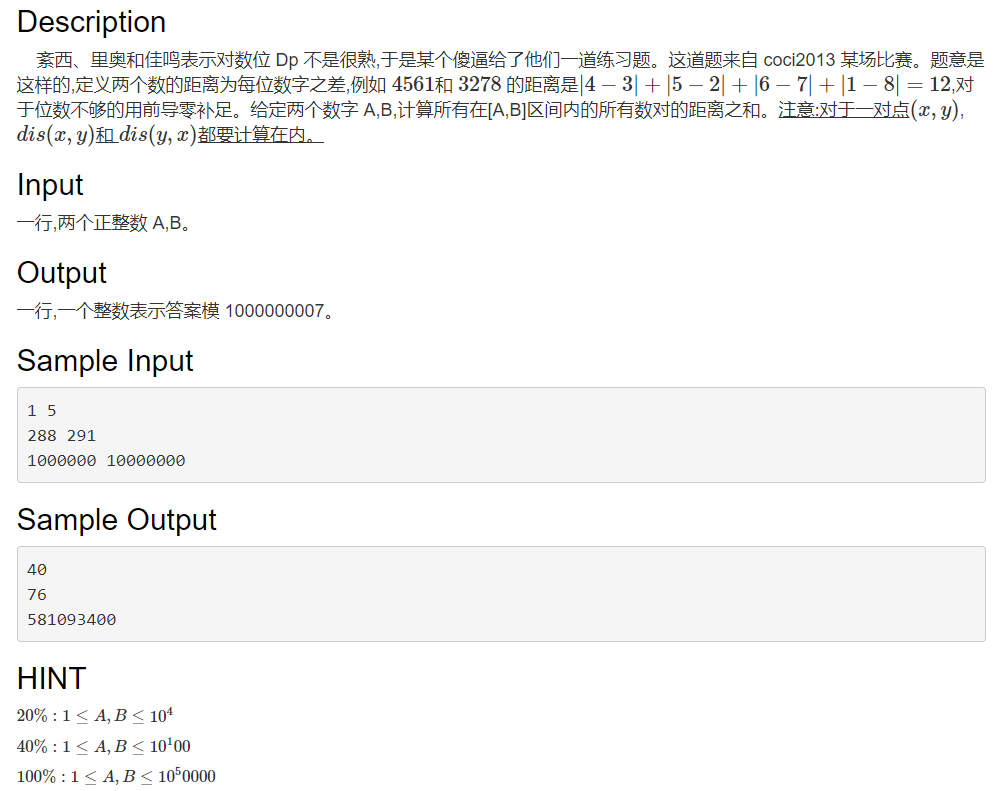
这题是显然的数位$dp$，然而我居然写了一个下午！！！

我们不难想到差分，令$solve(x,y)$表示从第一个数字在区间$[0,x]$，第二个数字在区间$[0,y]$的答案。

不难发现题目中给了你一对$A$,$B$，答案显然为$solve(B,B)-2solve(A-1,B)+solve(A-1,A-1)$。

考虑如何求解$solve(x,y)$函数，令$n=max(len(x),len(y))$，其中$len(p)$表示数字$p$在十进制下的长度（以下的位均代表十进制位）。

令$f[i]$表示数字$x$在模意义下前$i$位的值，令$F[i]$表示数字$x$在模意义下后$n-i+1$位的值。

同理，我们处理出$g[i]$和$G[i]$。

令$mi[i]$表示模意义下$10^i$的值，$Mi[i]$表示模意义下$10^(n-i+1)$的值。

令$ans[i][j][k]$表示第一个数字的第$i$位为$j$，第二个数字的第$i$位为$k$时的答案。

设第一个数字第$i$位为$j$的数字个数为$mul1$，第二个数字第$i$位为$k$的个数为$mul2$。

下面考虑如何求$mul1$，设$x[i]$为数字$x$的第i位，$num[i]$为数字$x$前$i$位构成的数，$Num[i]$为数字$x$后$i$位构成的数。

当$x[i]<j$时，$mul1=(f[i-1]+1)\times Mi[i+1]$，这里可以理解为前$i$位填一个数不大于$num[i-1]$的数，或者全填$0$，后$n-i$个数随便填的方案数。

当$x[i]==j$时，$mul1=f[i-1]\times Mi[i+1]+F[i+1]+1$ ，这里可以理解为前$i$位填一个小于$num[i-1]$的数，后$n-i$个数随便填的方案数，加上前$i$个数和$x$的前i个数相同，后n-i个数填写不大于F[i+1]的方案数。

当x[i]>j时，$mul1=f[i-1]\times Mi[i+1]$，这里可以理解为前$i$位填一个小于$num[i-1]$的数,后$n-i$位随便填的方案数。

求$mul2$同理

那么显然，$ans[i][j][k]=mul1\times mul2$。$solve(x,y)=\sum_{i=1}^{n}\sum_{j=0}^{9}\sum_{k=0}^{9}ans[i][j][k]$。

最终的答案为$solve(B,B)-2solve(A-1,B)+solve(A-1,A-1)$。考虑到$A$跟$B$的位数可能很大，这个减法需要用高精度。

完结撒花，注意细节。

 #include<bits/stdc++.h>
 #define MOD 1000000007
 #define M 100005
 #define LL long long
 using namespace std;
 char c[M]={};
 struct bign{
     LL a[M+],len; bign(){memset(a,,sizeof(a));}
     void rd(){
         scanf("%s",c); len=strlen(c);
         for(LL i=;i<len;i++) a[M-i]=c[len-i-]-'';
     }
     void jian(){
         for(LL i=M,g=;i&&g;i--){
             LL s=a[i]-g;
             if(s>=) a[i]=s,g=;
             else a[i]=s+,g=;
         }
         for(LL i=;i<=M;i++)
         if(a[i]!=){
             len=M-i+;
             return;
         }
     }
 }A,B,L,R;
 LL f[M]={},g[M]={},F[M]={},G[M]={},mi[M]={},Mi[M]={},a[M]={},b[M]={},n;
 
 LL solve(){
     n=max(A.len,B.len); LL res=;
     mi[]=; for(LL i=;i<=n;i++) mi[i]=mi[i-]*%MOD;
     F[n+]=G[n+]=;
     for(LL i=;i<=n;i++) a[i]=A.a[M-n+i],b[i]=B.a[M-n+i];
     for(LL i=;i<=n;i++) f[i]=(f[i-]*+a[i])%MOD,g[i]=(g[i-]*+b[i])%MOD;
     for(LL i=n;i;i--) F[i]=(F[i+]+a[i]*mi[n-i])%MOD,G[i]=(G[i+]+b[i]*mi[n-i])%MOD;
     Mi[n+]=; for(LL i=n;i;i--) Mi[i]=Mi[i+]*%MOD;
 
     for(LL i=;i<=n;i++){
         for(LL num1=;num1<;num1++)
         for(LL num2=;num2<;num2++){
             LL cha=abs(num1-num2),mul1=,mul2=;
             if(num1<a[i]) mul1=(f[i-]+)*mi[n-i]%MOD;
             if(num1==a[i]) mul1=(f[i-]*Mi[i+]%MOD+F[i+]+)%MOD;
             if(num1>a[i]) mul1=f[i-]*Mi[i+]%MOD;
 
             if(num2<b[i]) mul2=(g[i-]+)*mi[n-i]%MOD;
             if(num2==b[i]) mul2=(g[i-]*Mi[i+]%MOD+G[i+]+)%MOD;
             if(num2>b[i]) mul2=g[i-]*Mi[i+]%MOD;
 
             res=(res+mul1*mul2%MOD*cha)%MOD;
         }
     }
     return res;
 }
 
 int main(){
     L.rd(); R.rd();
     LL ans=;
     A=R; B=R;
     ans=solve();
     A=L; A.jian();
     ans=(ans-*solve()+*MOD)%MOD;
     B=L; B.jian();
     ans=(ans+solve())%MOD;
     cout<<ans<<endl;
 }