Codeforces70 | Codeforces Beta Round #64 | 瞎讲报告

目录

• 前言
• 正文
  • A
  • B
  • C
  • D
  • E

前言

这个毒瘤的517 放了Div1
然后D题是昨天讲的动态凸包（啊喂！我还没来的及去写
结果自己想的是二分凸包 （当然没有写出来
写完前两题之后就愉快地弃疗
C题也没有想出来 我真是太菜了呀
所以从C开始详写

正文

A

很明显的* 3 * 3 * 3...吧

B

只需求出每个句子多少长 然后贪心尽量多选几个句子到一段里就行了啊

C

题意

有序二元组\((x,y)\) 满足\(x*y=rev(x)*rev(y)\) 则称其是幸运的
\(rev(x)\) 表示x的反向 举个例子 rev(123456789)=987654321,rev(1200)=21
满足\(x \leq maxx,y \leq maxy\) 对于所有的对\((i,j)\) (\(i \leq maxx\),\(j \leq maxy\)) 中的幸运对至少有\(w\)
求\(x*y\)最小时的\(x,y\)
给出\(maxx,maxy,w\)

数据约束

\(maxx,maxy \leq 10^5,w \leq 10^7\)

解析

因为\(i*j=rev(i)*rev(j)\)可以推出\((\frac{i}{rev(i)})* (\frac{j}{rev(j)})=1\)
那这个本质上是不是就是在一个长为\(maxx\)宽为\(maxy\)的矩形里面截取一个长为\(i\)宽为\(j\)的矩形

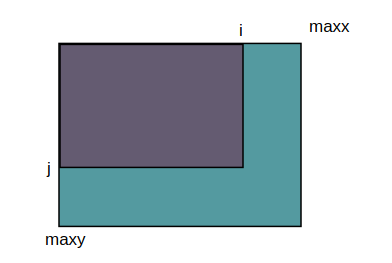
我们可以把\(rev(i)\)和\(i\)映射到一个map里面
然后用two-pointer去扫即可
（对于长度为\(k\)最少的宽度为\(t\) 那么显然对于长度为\(k-1\)所对应的宽度\(pos\) 有\(t \leq pos\)

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
int rev[N],A[15];
LL qx[N];
int bx=-1,by=-1;
map<LL,LL>mp,pp;

int Rev(int x){
    A[0]=0;
    for(;x;x/=10) A[++A[0]]=x%10;
    int pos=0,kk=1;
    rf(i,A[0],1) pos+=A[i]*kk,kk*=10;
    return pos;
}

int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}

void fail(){
    printf("-1\n");
    exit(0);
}

void UPD(int x,int y,int z){
    int gg=gcd(max(x,y),min(x,y));
    x/=gg,y/=gg;
    LL pos=x*1LL*100000+y;
    mp[pos]+=z;
}

void Cha(int x,int y,int z){
    int gg=gcd(max(x,y),min(x,y));
    x/=gg,y/=gg;
    LL pos=x*1LL*100000+y;
    pp[pos]+=z;
}

LL Get(int x,int y){
    int gg=gcd(max(x,y),min(x,y));
    x/=gg,y/=gg;
    LL pos=y*1LL*100000+x;
    if(!mp.count(pos)) return 0LL;
    return mp[pos];
}

LL Ask(int x,int y){
    int gg=gcd(max(x,y),min(x,y));
    x/=gg,y/=gg;
    LL pos=y*1LL*100000+x;
    if(!pp.count(pos)) return 0LL;
    return pp[pos];
}

int main(){
    int maxx,maxy,w;
    cin>>maxx>>maxy>>w;
    fr(i,1,max(maxx,maxy)) rev[i]=Rev(i);
    fr(i,1,maxx) UPD(i,rev[i],1);
    LL pos=-1,nw=0,maxn=1e11;
    fr(i,1,maxy){
        Cha(i,rev[i],1);
        nw+=Get(i,rev[i]);
        //cout<<"i="<<i<<"nw="<<nw<<endl;
        if(nw>=w) {
            pos=i;
            maxn=min(maxn,pos*maxx);
            bx=maxx,by=pos;
            UPD(maxx,rev[maxx],-1);
            nw-=Ask(maxx,rev[maxx]);
            break;
        }
    }
    //cout<<nw<<endl;
    if(pos==-1) fail();
    rf(i,maxx-1,1){
        while(nw<w&&pos<maxy){
            pos++;
            Cha(pos,rev[pos],1);
            nw+=Get(pos,rev[pos]);
        }
        //cout<<i<<" "<<pos<<" "<<nw<<endl;
        if(nw<w) break;
        if(maxn>pos*1LL*i) maxn=pos*1LL*i,bx=i,by=pos;
        nw-=Ask(i,rev[i]);
        UPD(i,rev[i],-1);
    }
    printf("%d %d\n",bx,by);
    return 0;
}

代码是越写越丑了TAT

D

凸包 极角序 set

题意

一开始给你三个点 维护一个凸包
每次有两种操作

• 询问(x,y)是否在凸包内
• 加入点(x,y) 重新维护凸包

数据约束

\(3 \leq q \leq 10^5,-1e6 \leq x,y \leq 1e6\)

解析

发现各位大爷的代码都写得好简洁啊

由于太菜了 于是乎当场倒地去世

先选取一个凸包内部的点作为极角序的极点
用atan2(x,y)计算角度
这样每次询问一个点 我们都可以在set里面找到它的前驱与后驱（用lower_bound找
如果是插入 那么往两边判断叉积
可以写一个这样的函数 那么往前继续找前驱 或者往后找后驱只需调用一下就可以了TAT骚操作

it L(it x){
    if(x==st.begin()) x=st.end();
    x--;
    return x;
}

it R(it x){
    x++;
    if(x==st.end()) x=st.begin();
    return x;
}

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<set>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define db double
#define LL long long
using namespace std;
struct data{
    LL x,y,dis;
    db Arg;
}a[10],o,p;
set<data>qx;
typedef set<data>::iterator sit;

bool operator < (const data &a,const data &b){    //按角度排序 相等再按长度排序
    return a.Arg<b.Arg||(a.Arg==b.Arg&&a.dis<b.dis);
}

LL Cross(data pp,data A,data B){
    return (A.x-pp.x)*(B.y-pp.y)-(A.y-pp.y)*(B.x-pp.x);
}

sit L(sit x){
    if(x==qx.begin()) x=qx.end();
    x--;
    return x;
}

sit R(sit x){
    x++;
    if(x==qx.end()) x=qx.begin();
    return x;
}

LL pf(LL x){
    return x*x;
}

LL Dis(data A,data B){
    return pf(A.x-B.x)+pf(A.y-B.y);
}

int main(){
    int q;cin>>q;
    fr(i,1,3){
        int tp;
        scanf("%d%lld%lld",&tp,&a[i].x,&a[i].y);
        o.x+=a[i].x,o.y+=a[i].y;
        a[i].x*=3,a[i].y*=3;
    }
    fr(i,1,3){
        a[i].dis=Dis(o,a[i]);
        a[i].Arg=atan2(a[i].y-o.y,a[i].x-o.x);
        qx.insert(a[i]);
    }
    q-=3;
    fr(cse,1,q){
        int tp;
        scanf("%d%lld%lld",&tp,&p.x,&p.y);
        p.x*=3,p.y*=3;
        p.Arg=atan2(p.y-o.y,p.x-o.x);
        p.dis=Dis(p,o);
        sit i=qx.lower_bound(p),j;
        if(i==qx.end()) i=qx.begin();
        j=L(i);
        if(tp==2){
            if(Cross(*j,p,*i)<=0) printf("YES\n");
            else printf("NO\n");
            continue;
        }
        if(Cross(*j,p,*i)<=0) continue;
        qx.insert(p);
        sit pos=qx.find(p);
        i=L(pos);j=L(i);
        while(Cross(*j,*i,*pos)<=0){
            qx.erase(i);
            i=j;j=L(j);
        }
        i=R(pos),j=R(i);
        while(Cross(*j,*i,*pos)>=0){
            qx.erase(i);
            i=j;j=R(j);
        }
    }
    return 0;
}

E

树型dp 输出路径

题意

给你一棵树\(n\)个节点
可以在节点中建立关键点 每建立一个关键点的花费为\(k\)
然后节点到最近的那个关键点获取信息 代价为\(d_len\)
给出\(d\)数组 求最小花费 并输出每个节点的到那个关键点获取信息

数据约束

\(1 \leq n \leq 180,d_i<d_{i+1}\)

解析

感觉不是一道很难的DP吧 但我一开始以为数据范围是1e5的TAT
设\(dp[u][i]\)表示给\(i\)建立关键点 \(u\)到\(i\)获取信息 \(u\)的子树的最小代价
\(ans[u]\)则表示\(dp[u][i]\)最小所对应的\(i\)

考虑从\(u\)的儿子\(s\)转移到\(u\)
\[dp[u][i]=k+d[dis[u][i]]\]
\[dp[u][i]+=min(dp[s][ans[s]],dp[s][i]-k)\]

然后输出路径的时候 就看是\(dp[s][ans[s]]\)小一点还是\(dp[s][i]-k\)小一点的

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i<=y;++i)
#define LL long long
using namespace std;
const int N=210;
int dp[N][N],ans[N],d[N][N],w[N],f[N];
int n,k;

void dfs(int u,int fa){
    fr(s,1,n) if(d[u][s]==1&&s!=fa) dfs(s,u);
    fr(i,1,n){
        int pos=w[d[u][i]]+k;
        fr(s,1,n){
            if(d[u][s]==1&&s!=fa){
                pos+=min(dp[s][i]-k,dp[s][ans[s]]);
            }
        }
        dp[u][i]=pos;
    }
    ans[u]=1;
    fr(i,2,n) if(dp[u][ans[u]]>dp[u][i]) ans[u]=i;
}

void sc(int u,int fa){
    if(dp[u][ans[u]]<=dp[u][f[fa]]-k) f[u]=ans[u];
    else f[u]=f[fa];
    fr(i,1,n)
        if(d[u][i]==1&&i!=fa) sc(i,u);
}

int main(){
    scanf("%d%d",&n,&k);
    fr(i,1,n-1) scanf("%d",&w[i]);
    memset(d,0x3f,sizeof d);
    for(int i=1,x,y;i<n;++i){
        scanf("%d%d",&x,&y);
        d[x][y]=1,d[y][x]=1;
    }
    fr(i,1,n) d[i][i]=0;
    fr(k,1,n) fr(i,1,n) fr(j,1,n) d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    dfs(1,0);
    cout<<dp[1][ans[1]]<<endl;
    f[1]=ans[1];
    fr(i,1,n) if(d[i][1]==1) sc(i,1);
    fr(i,1,n) printf("%d ",f[i]);
    return 0;
}