[CREC2007/CQOI2014]robotic sort

Description

一个实验室里有n个长短不一的试管。你的任务是编写一段程序，用机器臂把它们按照高度从小到大的顺序排列。

对于高度相同的试管，排序前后的相对位置应保持不变。排序方法如图所示。



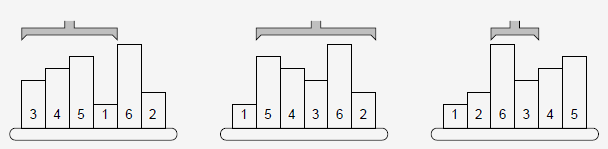
排序需要n次操作，其中第i次操作是反转序列i ~ Pi，其中Pi是目标状态中第i个试管当前所在的位置。比如，在上图中，初始时P1=4，因此反转试管1 ~ 4就能把最左边的试管归位。类似地，第2次操作前P2=6，因此反转2 ~ 6就能把左数第2个试管归位。你的任务是输出P1,P2,…,Pn的值，以便控制机器臂移动。注意i=Pi时实际上不需要反转，但仍然需要输出Pi。

Input

输入包含多组测试数据。每组数据第一行为试管个数n(1≤n≤100000)，第二行从左到右依次为每个试管的高度。输入以0结束。

Output

对于每组数据输出一行，依次为P1,P2,…,Pn。

Sample Input

6

3 4 5 1 6 2

4

3 3 2 1

0

Sample Output

4 6 4 5 6 6

4 2 4 4

---

记录一个pos[x]，代表以x为根的子树内的最小编号，那么每次查询[i,n]中的最小值，然后把该点splay到根后，左子树的大小就是答案，然后维护一个翻转标记即可。建树的时候不能建成一条链，要递归建成一棵树

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e5;
struct AC{
	int val,pos;
	void join(int i){val=read(),pos=i;}
}A[N+10];
bool cmp(AC x,AC y){return x.val!=y.val?x.val<y.val:x.pos<y.pos;}
bool cmp1(AC x,AC y){return x.pos<y.pos;}
struct Splay{
	#define T(x) (tree[f[x]][1]==x)
	#define ls (tree[x][0])
	#define rs (tree[x][1])
	int tree[N+10][2],f[N+10],size[N+10],Min[N+10],v[N+10],pos[N+10],ans[N+10];
	bool flag[N+10];
	int root,n;
	void updata(int x){
		size[x]=size[ls]+size[rs]+1;
		Min[x]=v[x],pos[x]=x;
		if (Min[x]>Min[ls]){Min[x]=Min[ls];pos[x]=pos[ls];}
		if (Min[x]>Min[rs]){Min[x]=Min[rs];pos[x]=pos[rs];}
	}
	void pushdown(int x){
		if (!flag[x])	return;
		flag[ls]^=1;
		flag[rs]^=1;
		swap(ls,rs);
		flag[x]=0;
	}
	void build(int fa,int l,int r){
		if (l>r)	return;
		if (l==r){
			f[l]=fa,size[l]=1;
			l<fa?tree[fa][0]=l:tree[fa][1]=l;
			v[l]=Min[l]=A[l].val,pos[l]=l;
			return;
		}
		int mid=(l+r)>>1;
		build(mid,l,mid-1),build(mid,mid+1,r);
		f[mid]=fa,v[mid]=A[mid].val;
		mid<fa?tree[fa][0]=mid:tree[fa][1]=mid;
		updata(mid);
	}
	void move(int x){
		int fa=f[x],son=tree[x][T(x)^1];
		tree[x][T(x)^1]=fa;
		tree[fa][T(x)]=son;
		if (son)	f[son]=fa;
		f[x]=f[fa];
		if (f[x])	tree[f[x]][T(fa)]=x;
		f[fa]=x;
		updata(fa),updata(x);
	}
	void up(int x){
		if (!x)	return;
		up(f[x]);
		pushdown(x);
	}
	void splay(int x){
		up(x);
		while (f[x]){
			if (f[f[x]])	T(x)==T(f[x])?move(f[x]):move(x);
			move(x);
		}
		root=x;
	}
	int find(int x,int i){
		if (!i)	return 0;
		pushdown(i);
		if (size[tree[i][0]]+1==x)	return i;
		if (x<=size[tree[i][0]])	return find(x,tree[i][0]);
		return find(x-size[tree[i][0]]-1,tree[i][1]);
	}
	void filp(int x,int y){
		x=find(x,root),splay(x);
		y=find(y+2,root),splay(y);
		if (f[x]!=root)	move(x);
		flag[tree[x][1]]^=1;
	}
	int query(int x,int y){
		x=find(x,root),splay(x);
		y=find(y+2,root),splay(y);
		if (f[x]!=root)	move(x);
		return pos[tree[x][1]];
	}
	void init(){
		n=read(),root=(n+3)>>1;
		if (!n)	exit(0);
		A[1].val=A[n+2].val=Min[0]=inf;
		for (int i=2;i<=n+1;i++)	A[i].join(i);
		sort(A+2,A+2+n,cmp);
		for (int i=2;i<=n+1;i++)	A[i].val=i;
		sort(A+2,A+2+n,cmp1);
		build(0,1,n+2);
	}
	void work(){
		init();
		for (int i=1;i<=n;i++){
			int x=query(i,n);
			splay(x);
			ans[i]=size[tree[x][0]];
			filp(i,ans[i]);
		}
		for (int i=1;i<=n;i++)	i!=n?printf("%d ",ans[i]):printf("%d\n",ans[i]);
	}
}T;
int main(){
	T.work();
	return 0;
}