P4138 [JOISC2014]挂饰

P4138 [JOISC2014]挂饰

◦          N个装在手机上的挂饰。挂饰附有可以挂其他挂件的挂钩。每个挂件要么直接挂在手机上，要么挂在其他挂件的挂钩上。直接挂在手机上的挂件最多有1个。此外，每个挂件有一个安装时会获得的喜悦值，用一个整数来表示，可能为负。

◦          想要选出一些挂饰挂在一起，最大化所有挂饰的喜悦值之和。

◦          1<=N<=2000
           0<=Ai<=N(1<=i<=N)表示挂勾的数量
           -10^6<=Bi<=10^6(1<=i<=N)表示喜悦值。

>Solution

◦          首先贪心的想，如果最终选出的一组挂饰，肯定是从上到下先挂所含挂钩多的。所以先按照挂钩数量从大到小排序。

Why？？

（1）0       100   挂钩数  喜悦值

（2）1  100

乱序ans为100

◦          然后设dp[i][j]前i个挂饰，剩余j个挂钩的最大喜悦值是多少即可。

◦          转移枚举下一个挂饰是否挂。

◦          挂，挂钩数更新就 j - 1 + a[i+1]，对应的修改喜悦值；不挂，挂钩数就直接转移过来

但是这个值可能是个负数啊，dp[i][0]就不能转移了啊

◦        转移方程： dp[i][j]=max(dp[i-1][j],dp[i-1][max(j-a[i],0) +1]+v[i])

注意此处为什么是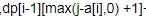这个+1放在外面呢？？？

假设我们挂第 i 个挂饰，那么挂之前有 i-1 个挂饰，有 x 个挂饰，那么 x-1+a[i]=j，

因为挂上第 i 个挂饰要消耗一个挂钩，然后你会得到第 i 个挂饰的挂钩

所以 x = j - a[i] + 1

j-a[i]有可能是负数，一旦是负数，那肯定就不存在此情况，就相当于你把之前的挂饰全从手机上卸下来，然而手机默认自己就有一个挂钩，所以+1放到外面

◦          注意dp[i][0]不能转移。

状态设计充分描述尽量简洁，什么影响问题就把什么记下来

PS：奉劝各位 f 数组一定要初始化最小值！！！

        memset(f,-0x3f3f3f3f,sizeof(f))

       （不过你初始化的这个值并不等于-0x3f3f3f3f,是一个绝对值较大的负数

       （这个T我写的-0x3f没有事,因为memset是用最后两位来填充的数组

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=,minn=-;
int n,ans=;
int f[maxn][maxn];
struct node
{
    int a,b;
}gou[maxn];

bool cmp(node x,node y)
{
    if(x.a==y.a) return x.b >y.b ;
    return x.a >y.a ;
}

int main()
{
    n=read();
    for(int i=;i<=n;i++)
      gou[i].a =read(),gou[i].b=read();
    sort(gou+,gou+n+,cmp);
    memset(f,-0x3f,sizeof(f));

    f[][]=;

    for(int i=;i<=n;i++)
      for(int j=;j<=n;j++)
      f[i][j]=max(f[i-][j],f[i-][max(j-gou[i].a,)+]+gou[i].b );

    for(int i=;i<=n;i++)
      ans=max(ans,f[n][i]);
    printf("%d",ans);
    return ;
}