Introduction to Mathematical Thinking - Week 9 评论答案2

根据 rubic 打分。

1.

我认为，如果说明 m, n 是自然数，所以最小值是 1 会更清楚。所以 Clarity 我给了 3 分。其他都是 4 分，所以一共是 23 分。

2. 

我给出的分数 0 + 4 + 4 + 4 + 4 + 0。

明显可以看出是计算错误，但由于目前是考察数学思考，并不需要像工程师一样精确。所以这个被视为 slip。

Logical correctness: 2 分。逻辑正确但是计算错误。

Overall valuation: 2 分。同理，逻辑正确但是计算错误。

3. 

我给出的分数：4 + 3 + 4 + 3 + 4 + 2 = 20

下结论那里写的是 n(n+1) 而实际上应该是 n^2 + n + 1。

所以， clarity 是 3分，需要花一点点来弄清楚结论。

State conclusion 是 3 分，需要花一点点来弄清楚结论。

Overall valuation 是 2 分。The answer is fairly good, but there is room for improvement.

4. 

没有理解题意，0分。

5. 

我给出的分数：4 + 4 + 3 + 0 + 4 + 2

开头的结论，少了理由 "By the Division Theorem"

Clarity: 开头的结论，少了理由 "By the Division Theorem"，所以给 3 分。你不说原因，会令人困惑。

Opening: 3 分。同样的理由

State conclusion：3 分。有隐含提到，我认为给 2 分就够了。

Reasons：0分。同样的理由，因为缺少重要的理由（前提）。

Overal： 2 分。有提升空间。

4 + 3 + 3 + 3 + 0 + 2 = 15

6. 

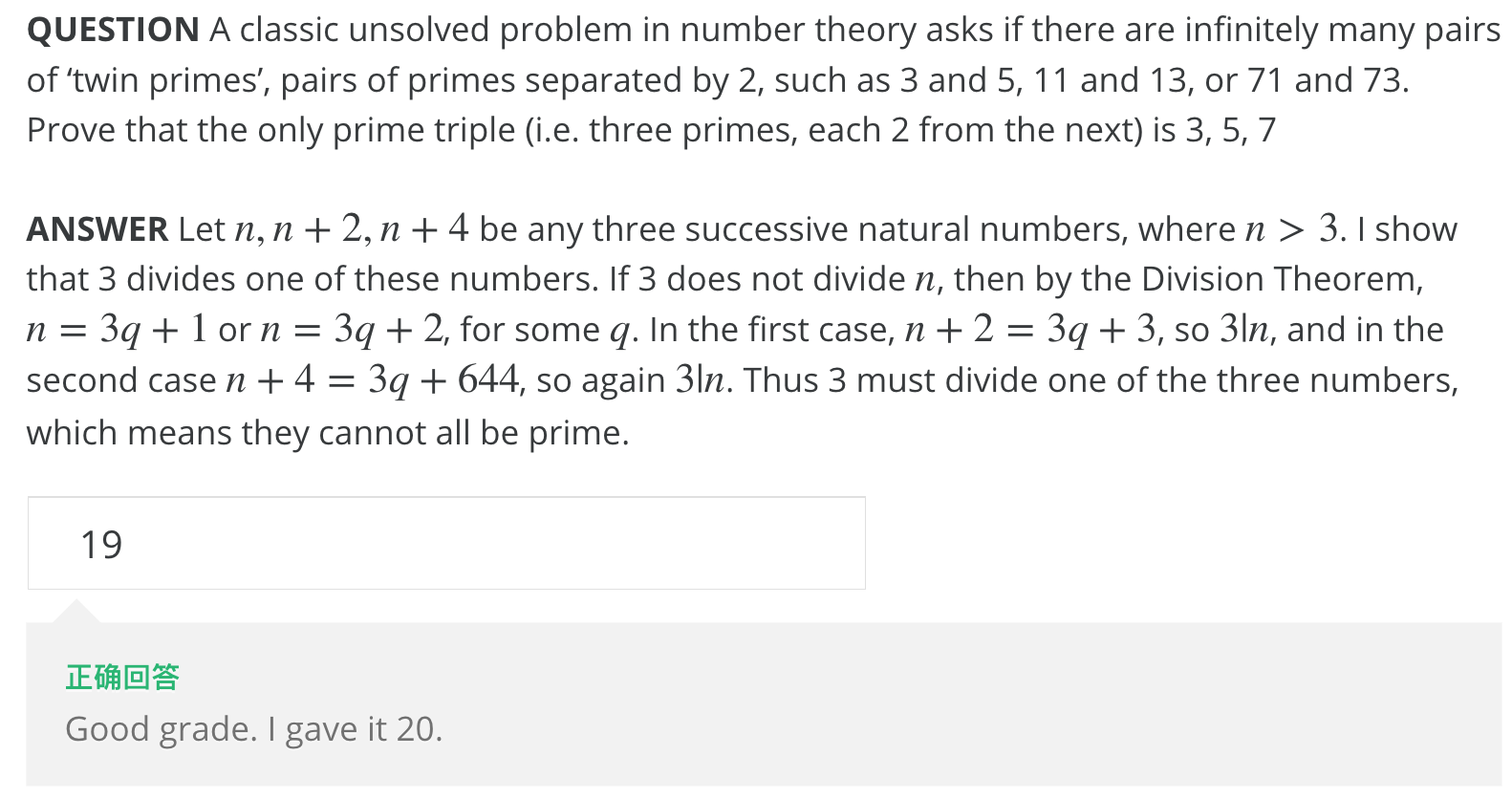
我的评分：4 + 4 + 3 + 2 + 4 + 2

评分存在问题，Opening 中，引用了 Division Theorem，给 4 分。State conclusion 给 4 分，"they can not all be prime"。

虽然存在很多 typos，但是逻辑是正确的。但对于我来说，这些 typo 让我花费更多去理解，所以 Clarity 给 2 分，Overall valuation 给 2 分。

7.

我给出的评分：4 + 4 + 4 + 0 + 4 + 2

在 "Assume it hold for n. Then" 之后，少了 "adding 2^(n+1) to both side of the assumed identity"，所以会令人很困惑。由于这个

Clarity: 2 分

Reasons: 2 分

Overall valuation: 2 分

其他都是 4 分。至于我认为的没有陈述结论，其实逻辑上已经完整了。"The result(assumption) follows by induction"。所以总分相同，可能错的更离谱。

8. 

我给出了满分。

Instructor 认为："Pick epsolon > 0" 会让初学者困惑，应该换成 "Let epsolon > 0 be given"，因为这个 proof 是写给人看的，目标群体是初学者。

最后的结论少了 "by definition of limits"。

所以 Clarity, Opening, Reasons, Overall Valuation 都是 3 分。总分为 20。

9. 

我给出的评分：4 + 3 + 4 + 3 + 3 + 4

对于初学者来说，还需要证明趋近于 0 为什么交集是空集。所以 Clarity 是 3 分，Reasons 是 2 分，Overall valuation 是 3 分。

10.

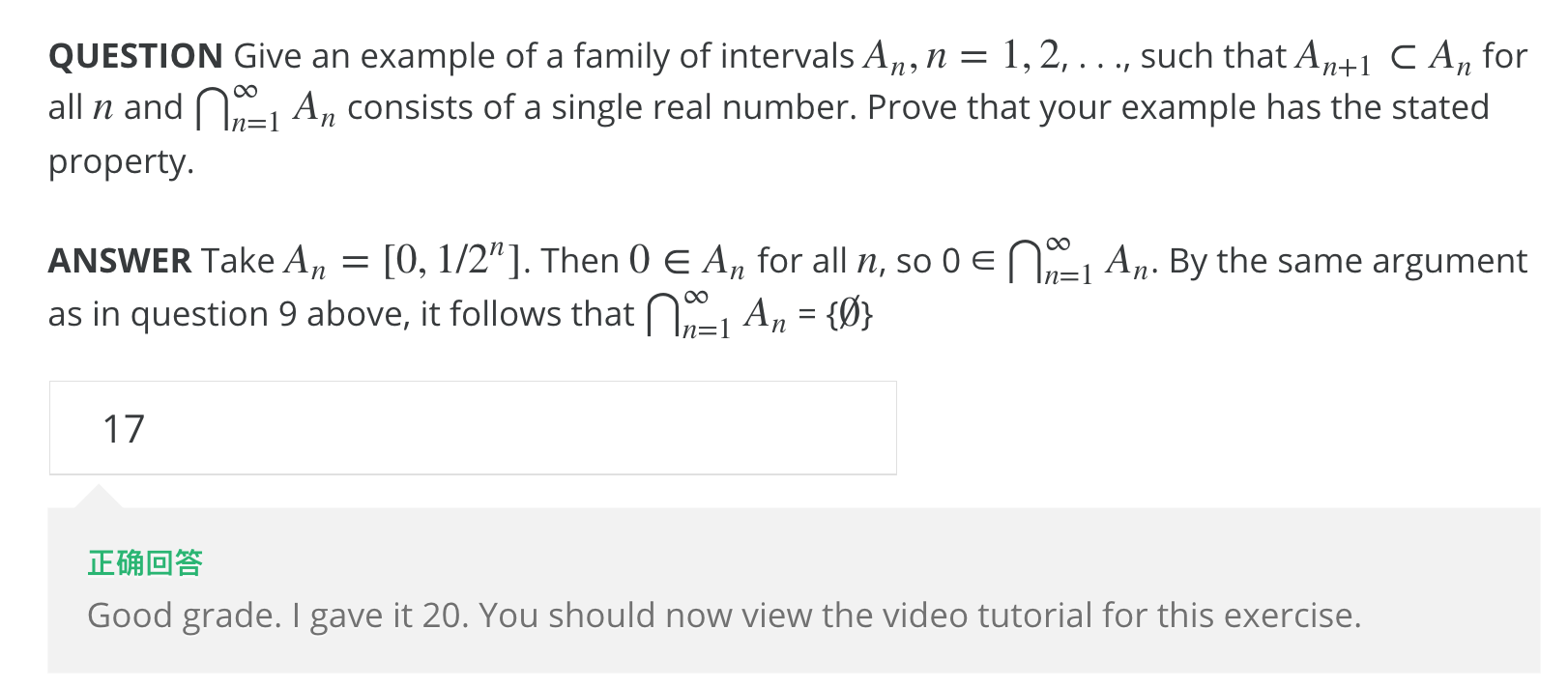
和上一题一样。