【题解】Digit Tree

【题解】Digit Tree

CodeForces - 716E

呵呵以为是数据结构题然后是淀粉质还行...

题目就是给你一颗有边权的树，问你有多少路径，把路径上的数字顺次写出来，是\(m\)的倍数。

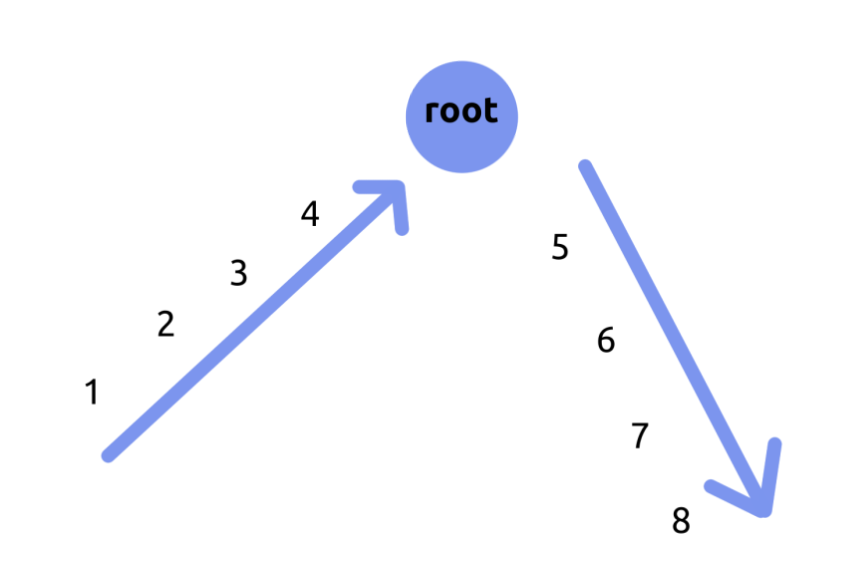
很明显可以点分治嘛，我们可以按照图上的样子，把一条路径本来是\(12345678\)的路径，变成\(1234|5678\)，我们记录图中左边的那种路径为\(f\)(往根)，右边的那种路径为\(g\)(从根)，记右边的那种到分治中心的深度为\(d\)，那么这条路径就可以被表示成\(f\times 10^d+g\)，条件就变成了

\[f \times 10^d +g\equiv 0
\\
f \times 10^d \equiv -g
\\
f \equiv -g \times 10^{-d}
\]

我们把坐边压到一个\(map\)里面，每次分治时拿右边直接枚举就好了，然后还要用第二个\(map\)去掉同一颗子树内的非法情况，具体实现看代码。

由于处理这个\(f,g\)真的很难(博主搞了好久，自己都晕了)，所以代码里的\(f,g\)可能是反的...

不觉得难的可以自己去试试，如果你真的没晕的话..收下我的膝盖orz

咱们把\(map\)看做一个\(log\)，时间复杂度就是\(O(n \log^2n)\)的

#include<bits/stdc++.h>
using namespace std;  typedef long long ll;
template < class ccf > inline ccf qr(ccf ret){      ret=0;
      register char c=getchar();
      while(not isdigit(c)) c=getchar();
      while(isdigit(c)) ret=ret*10+c-48,c=getchar();
      return ret;
}
const int maxn=1e5+5;
typedef pair < int , ll > P;
vector < P > e[maxn];
vector < int > ve;
#define pb push_back
#define st first
#define nd second
#define mk make_pair
inline void add(int fr,int to,int w){
      e[fr].pb(mk(to,w));
      e[to].pb(mk(fr,w));
}
int sum;
int siz[maxn];
int d0[maxn];//深度
int f[maxn];
int g[maxn];
int rt;
int spc[maxn];
int inv[maxn];
int ten[maxn];
bool usd[maxn];
int n,mod;
map < int , int > mp,un;
ll ans;

void dfsrt(const int&now){//重心
      usd[now]=1;
      siz[now]=spc[now]=1;
      for(auto t:e[now])
            if(not usd[t.first]){
                  dfsrt(t.st);
                  siz[now]+=siz[t.st];
                  if(siz[t.st]>spc[now])spc[now]=siz[t.st];
            }
      spc[now]=max(spc[now],sum-siz[now]);
      if(spc[now]<spc[rt]|| not rt) rt=now;
      usd[now]=0;
}

void dfsd(const int&now,const int& last,const int&w){//dis
      usd[now]=1;
      d0[now]=d0[last]+1;
      g[now]=(g[last]+1ll*ten[d0[last]]*w%mod)%mod;
      f[now]=(f[last]*10ll%mod+w)%mod;
      //printf("now=%d d0=%d f=%d g=%d\n",now-1,d0[now],f[now],g[now]);
      ans+=(f[now]==0)+(g[now]==0);
      ++un[g[now]];
      ++mp[g[now]];
      ve.pb(now);
      for(auto t:e[now])
            if(not usd[t.st])
                  dfsd(t.st,now,t.nd);
      usd[now]=0;
}

inline void calc(const int&now){
      d0[now]=f[now]=g[now]=0;
      ve.clear();mp.clear();
      int k=0;
      for(auto t:e[now])
            if(not usd[t.st]){
                  un.clear();
                  dfsd(t.st,now,t.nd);
                  register int edd=ve.size();
                  while(k<edd){
                        register int it=ve[k];
                        register int p=1ll*(((mod-f[it])%mod+mod)%mod)*inv[d0[it]]%mod;
                        if(un.find(p)!=un.end())
                              ans-=un[p];
                        ++k;
                  }
            }
      for(auto t:ve){
            register int p=1ll*(((mod-f[t])%mod+mod)%mod)*inv[d0[t]]%mod;
            if(mp.find(p)!=mp.end())
                  /*cout<<"?qaq="<<t-1<<' '<<p<<endl;*/
                  ans+=mp[p];
      }

}

void divd(const int&now){
      usd[now]=1;calc(now);
      for(auto t:e[now])
            if(not usd[t.st]){
                  sum=siz[t.st];rt=0;
                  dfsrt(t.st);
                  divd(rt);
            }
}

void exgcd(int a,int b,int&d,int&x,int&y){
      if(!b) d=a,x=1,y=0;
      else exgcd(b,a%b,d,y,x),y-=x*(a/b);
}

int Inv(const int&a, const int&p){
      int d,x,y;
      exgcd(a,p,d,x,y);
      return d==1?(x+p)%p:-1;
}

int main(){
      sum=n=qr(1);mod=qr(1);
      if(mod==1)return cout<<1ll*n*(n-1)<<endl,0;
      inv[0]=ten[0]=1;
      ten[1]=10;
      inv[1]=Inv(10,mod);
      if(inv[1]==-1)return -1;
      for(register int t=2;t<=n+1;++t)
            ten[t]=1ll*ten[t-1]*ten[1]%mod,inv[t]=1ll*inv[t-1]*inv[1]%mod;
      for(register int t=1,t1,t2,t3;t< n;++t){
            t1=qr(1)+1;t2=qr(1)+1;t3=qr(1);
            add(t1,t2,t3);
      }
      dfsrt(1);
      divd(rt);
      cout<<ans<<endl;
      return 0;
}