机器学习-5 支持向量机SVM
一、概念和背景
SVM:Support Vector Machine 支持向量机。
最早是由Vladimir N. Vapnik和Alexey Ya. Chervonenkis在1963年提出的。
目前的版本(soft margin)是由Corinna Cortes和Vapnik在1993年提出,并在1995年发表。
在深度学习(2012)出现之前,SVM被认为是机器学习中近十几年来最成功,表现最好的算法。
机器学习的一般框架:
训练集--->提取特征向量--->结合一定的算法(决策树、KNN等)--->结果
二、SVM
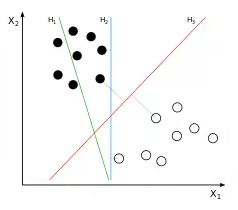
在上图中,我们有一些二维的样本,我们需要画一条线将他们区分开,现有绿色、蓝色、红色三条线,哪一条是最好的呢?
很明显,我们会认为红色线是最能明确划分两种样本的分界线。
我们将二维样本扩展到三维(三维空间)中,则这条红线会变成一个面红色的面,可以用来在三维空间中划分三维样本。
再将三维空间扩展为N维,则红色的面会变成一个超平面(hyper plane),这个超平面可以用来划分N维样本。
边际(margin):用于确定超平面位置,使不同类样本间边际(距离)最大。(例如黑点到白点的距离)
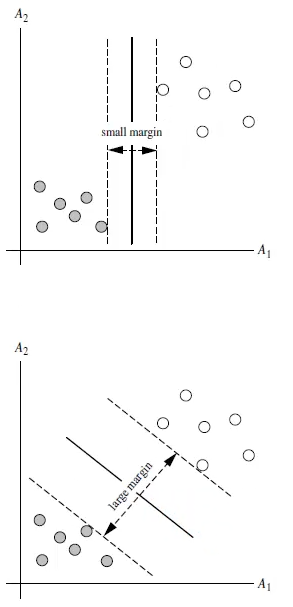
三、线性可区分和线性不可区分
线性可分:在样本空间中,可以使用一条直线(二维)、一个平面(三维)或一个超平面(N维)将样本区分开,叫做线性可区分。例如上面图中的情况。
线性不可分:不能使用一条直线(二维)、一个平面(三维)或一个超平面(N维)将样本区分开,叫做线性不可区分。如下图所示情况:
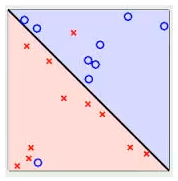
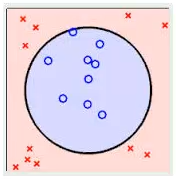
四、确定超平面
如何确定超平面:
用于划分样本的超平面可以有无数个,但是最优超平面是到不同类样本距离相等(并且边际最大)的超平面。
假设训练样本是二维的,X=(x1,x2);
1.超平面方程为:
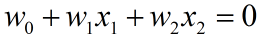
其中的w0相当于x0=1的情况。(和神经网络中的bias一样)
2.超平面两边的点满足:
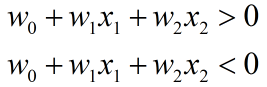
3.找到超平面两边的另外两个超平面:

所有坐落在该两个超平面(H1,H2)上的点被称作“支持向量(support vector)”。
4.分界超平面与处于H1和H2上的点(支持向量)的距离为:
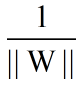
其中||W||是向量的范数,即模(norm)。
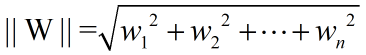
5.最大边际距离(H1到H2的距离)为:
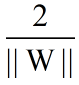
机器学习-5 支持向量机SVM的更多相关文章
- 机器学习算法 - 支持向量机SVM
在上两节中,我们讲解了机器学习的决策树和k-近邻算法,本节我们讲解另外一种分类算法:支持向量机SVM. SVM是迄今为止最好使用的分类器之一,它可以不加修改即可直接使用,从而得到低错误率的结果. [案 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 【机器学习】支持向量机SVM
关于支持向量机SVM,这里也只是简单地作个要点梳理,尤其是要注意的是SVM的SMO优化算法.核函数的选择以及参数调整.在此不作过多阐述,单从应用层面来讲,重点在于如何使用libsvm,但对其原理算法要 ...
- python机器学习之支持向量机SVM
支持向量机SVM(Support Vector Machine) 关注公众号"轻松学编程"了解更多. [关键词]支持向量,最大几何间隔,拉格朗日乘子法 一.支持向量机的原理 Sup ...
- 机器学习(十一) 支持向量机 SVM(上)
一.什么是支撑向量机SVM (Support Vector Machine) SVM(Support Vector Machine)指的是支持向量机,是常见的一种判别方法.在机器学习领域,是一个有监督 ...
- 机器学习:支持向量机(SVM)
SVM,称为支持向量机,曾经一度是应用最广泛的模型,它有很好的数学基础和理论基础,但是它的数学基础却比以前讲过的那些学习模型复杂很多,我一直认为它是最难推导,比神经网络的BP算法还要难懂,要想完全懂这 ...
- 机器学习(十一) 支持向量机 SVM(下)
支持向量机通过某非线性变换 φ( x) ,将输入空间映射到高维特征空间.特征空间的维数可能非常高.如果支持向量机的求解只用到内积运算,而在低维输入空间又存在某个函数 K(x, x′) ,它恰好等于在高 ...
- 吴裕雄--天生自然python机器学习:支持向量机SVM
基于最大间隔分隔数据 import matplotlib import matplotlib.pyplot as plt from numpy import * xcord0 = [] ycord0 ...
- 机器学习模型-支持向量机(SVM)
二.代码实现 import numpy as np from sklearn import datasets from sklearn.model_selection import train_tes ...
随机推荐
- c#调用ffmpeg嵌入srt/ass字幕提示Cannot load default config file...
c#调用ffmpeg嵌入srt/ass字幕提示 Fontconfig error: Cannot load default config file[Parsed_subtitles_0 @ 00000 ...
- c#开发移动APP-Xamarin入门扩展
原文:c#开发移动APP-Xamarin入门扩展 这节主要演示了如何通过添加第二个屏幕来跟踪应用程序的call历史来扩展Phoneword应用程序.最终如下: 按如下步骤扩展Phoneword 在Ph ...
- Linux性能测试 vmstat命令
vmstat命令是最常见的Linux/Unix监控工具,可以展现给定时间间隔的服务器的状态值,包括服务器的CPU使用率,内存使用,虚拟内存交换情况,IO读写情况.这个命令是我查看Linux/Unix最 ...
- Program for Linux USB-devices driver step by step (ONE)
Program for Linux USB-devices driver 開始啃硬骨头~ 这里我打算一步步给出USB device driver 的demo.希望有心能可以共同交流学习. 希望认识很多 ...
- 2-22-实现jsp通过tomcat连接mysql
所有软件的版本如下: MySQL-Connector-Java: mysql-connector-java-5.1.36 Tomcat: apache-tomcat-8.0.26 JDK: jdk-8 ...
- XF 通过判断平台加载不同的图片
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...
- Qt SQLite 批量插入优化(SQLite默认将每条语句看成单独的事务)good
使用SQLite存储数据时发现插入速度太慢,程序跑了将近五分钟才插入了不到三千条.上网查资料才发现,SQLite这种文件数据库与MySql机制不一样,每条事务都有打开和关闭文件的步骤,SQLite默认 ...
- OA 框架
@{ Layout = null;}<!DOCTYPE html><html><head> <meta name="viewport&q ...
- HTTP、FTP状态码 汇总
原文:HTTP.FTP状态码 汇总 HTTP1xx - 信息提示(这些状态代码表示临时的响应.客户端在收到常规响应之前,应准备接收一个或多个 1xx 响应. ) • 100 - 继续.• 101 - ...
- wcf中的消息模式
1请求响应模式 a.wcf中的消息模式默认是请求响应模式 b.返回值是void默认也是请求响应模式,可返回服务端的错误信息 c.客户端在请求后,当前线程停止真到接受收服务器的响应 [Opereatio ...
