POJ1463-Strategic game-（树形dp）

http://poj.org/problem?id=1463

题意：有一棵n个结点的树，要在这棵树上放士兵守卫，一个士兵可以守卫自己所在的位置以及与之相邻的点。问最少放多少个士兵？

题解：对于每个点，两种情况，放与不放，放则计数1，不放则计数0。

对于某个点x

如果不放，则与他相邻的点必然要放，否则谁来守卫点x？

如果放，则与他相邻的点可放可不放。

首先要造一棵树，从根节点对所有儿子节点深搜。

dp[i][0]和dp[i][1]表示 包括i本身 和 以i为父节点的子孙结点的摆放数 的累计最小值。

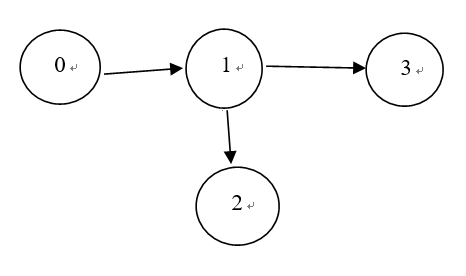
对于样例1，可以造出如下这样的树，0是根结点，指向儿子。

 #include<stdio.h>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<math.h>
 #include<string>
 #include<map>
 #include<queue>
 #include<stack>
 #include<set>
 #define ll long long
 #define inf 0x3f3f3f3f
 using namespace std;

 int n,m;
 int dp[][];
 vector<int>son[];
 bool vis[];

 void dfs(int x)
 {
     dp[x][]=;
     dp[x][]=;///每次进入深搜，初始化这个点是可以选或者不选
     for(int i=;i<son[x].size();i++)
     {
         int y=son[x][i];
         dfs(y);
         dp[x][]+=dp[y][]; ///如果不选，那么谁来守卫？那儿子就需要守卫
         dp[x][]+=min(dp[y][],dp[y][]);///如果选择守卫，则儿子可以选择守卫或者不守卫
     }
 }

 int main()
 {
     while(scanf("%d",&n)!=EOF)
     {
         for(int i=;i<n;i++)
             son[i].clear();
         memset(vis,false,sizeof(vis));
         memset(dp,,sizeof(dp));
         for(int i=;i<n;i++)
         {
             int x,y;
             scanf("%d:(%d)",&x,&m);
             while(m--)
             {
                 scanf("%d",&y);
                 son[x].push_back(y);
                 vis[y]=true;///y有父亲，不能作为根结点
             }
         }
         for(int i=;i<n;i++)
         {
             if(!vis[i])///找到没有儿子的结点作为根节点
             {
                 dfs(i);
                 printf("%d\n",min(dp[i][],dp[i][]));///取根节点的最小情况
                 break;
             }
         }
     }
     return ;
 }