[ACM][2018南京预赛]Lpl and Energy-saving Lamps

一、题面

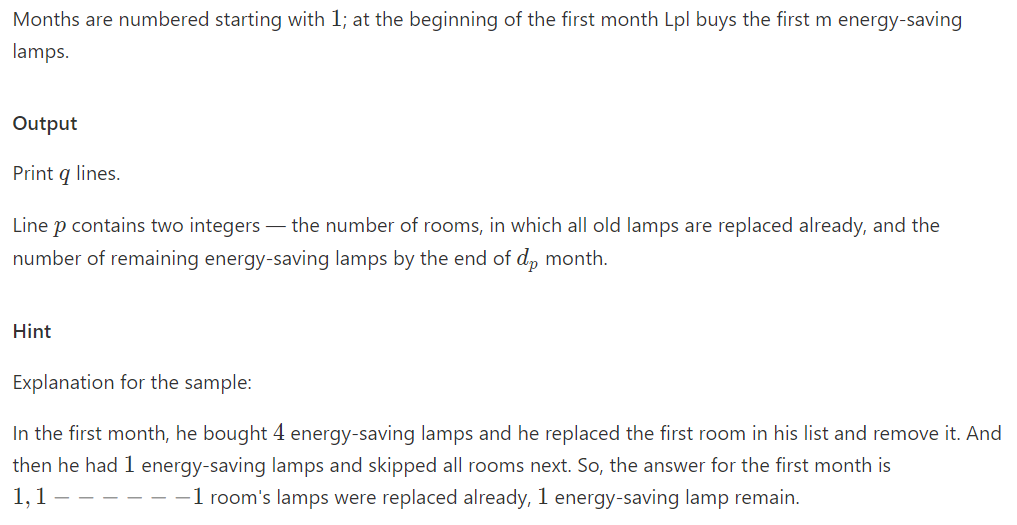
样例输入：

5 4
3 10 5 2 7
10
5 1 4 8 7 2 3 6 4 7

样例输出：

4 0
1 1
3 6
5 1
5 1
2 0
3 2
4 4
3 6
5 1

二、思路

关键词：线段树

这道题最难就难在看题吧。。。也许ACM的魅力之一便在于此——面对若干道题，你不知每一道题的难度是高是低，只能耐心地读清题面，审清题意，理清思路，方可知其是否在能力范围内以及预估耗时。考试过程中，我基本靠board来判断题目难度，清北大佬们先AC了哪些我就先做哪些。。。然而这道题似乎他们也不太愿意读题？其实际难度我觉得可能还要低于其他几道更早被A的题目。

题目大意是：现每个月提供m个灯泡，每次选出第一个小于当前灯泡数的房间，更换好该房间的灯泡，直至不存在这样的房间，则进入下个月。给出若干次月份数，求这几个月内能更换多少个房间的灯泡，以及剩余灯泡数。注意：当所有房间更换完之后，将不再提供灯泡！

n <= 10 ^ 5, d[p] <= 10 ^ 5，暴搜不可行。题目核心无非是求最早出现的小于k的数，可以用线段树维护每一段的最小值，再进行单点修改。水的一批。

三、代码

 #include <cstdio>
 #define MAXN 100005
 #define INF 0x3f3f3f3f

 int n, m, T, a[MAXN], x, t[MAXN << ], k, l[MAXN], r[MAXN], q, mx, tot;

 int max(int a, int b) {
     return a > b ? a : b;
 }

 int min(int a, int b) {
     return a < b ? a : b;
 }

 void build(int o, int l, int r) {
     if (l == r) {
         scanf("%d", &x), t[o] = x;
         return;
     }
     int m = (l + r) >> ;
     build(o << , l, m), build(o <<  | , m + , r);
     t[o] = min(t[o << ], t[o <<  | ]);
 }

 int query(int o, int l, int r) {
     if (l == r) return l;
     int m = (l + r) >> ;
     if (t[o] > k) return ;
     return t[o << ] <= k ? query(o << , l, m) : query(o <<  | , m + , r);
 }

 void upd(int o, int l, int r) {
     if (l == r) {
         k -= t[o], t[o] = INF;
         return;
     }
     int m = (l + r) >> ;
     if (q <= m) upd(o << , l, m);
     else upd(o <<  | , m + , r);
     t[o] = min(t[o << ], t[o <<  | ]);
 }

 void work() {
     for (int i = ; i <= mx; i++) {
         if (tot != n) {
             k += m;
             while (q = query(, , n)) upd(, , n), tot++;
         }
         l[i] = k, r[i] = tot;
     }
 }

 int main() {
     scanf("%d %d", &n, &m);
     build(, , n);
     scanf("%d", &T);
     for (int i = ; i <= T; i++) scanf("%d", &a[i]), mx = max(a[i], mx);
     work();
     for (int i = ; i <= T; i++) printf("%d %d\n", r[a[i]], l[a[i]]);
     return ;
 }