【学时总结】 ◆学时·III◆ 二分图

【学时·III】 二分图

---

■基本策略■

其实本质是图论中的网络流

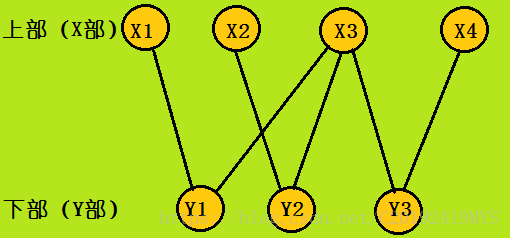
二分图是两个由多个点组成的集合（上部和下部，且没有重叠），两个集合中的点不与该集合内其他的点连通，但和另一个集合内的点连通。我们称这两个集合为上部、下部，或X、Y部，比如：

• 判定

我们可以通过染色的方法将一个普通的连通图转换为二分图（如果不是连通图，则说明该图存在多个二分图或不为二分图）。由于X部只与Y部相连，Y部也只与X部相连，我们可以把X、Y部染成不同的颜色。通过BFS(DFS也可以)从图里的一个点开始，假设它为X部，则与它相连的点为Y部，之后又为X部……直到访问到一个标记过的点，且该点的标记与将要作的标记不同，则不是二分图。将所有点标记完后还没有冲突，则是二分图。

• 算法

与二分图相关的有匈牙利算法、König定理，分别处理增广路和最大匹配问题。

• 最大匹配

二分图中若存在边集 E() 使得其中的边没有交点（共同的顶点），则称 E() 是该二分图的一个匹配。

特别的，若 E() 所含的顶点恰好是二分图中所有的顶点，则称 E() 为完全匹配。

最常考的是最大匹配，此时 E() 所包含的边的数量达到二分图中可能的最大数量。

• 增广路径

边集 E() 为二分图已经匹配的边，路径P连接不同部的未匹配的点，若在P中匹配的边和未匹配的边交替出现，则称P为增广路径。可见P的边数一定是奇数，且因为起点和终点都未匹配，所以匹配边比未匹配边少1。

通过将增广路径反色——未匹配边换为匹配边，匹配边换为未匹配边，我们可以得到一个更好的匹配。当没有增广路径时，形成的匹配就是该二分图的最大匹配。

这种算法称为匈牙利算法。

---

■来一点版题■

◆没有技术含量◆ eXam

只要知道二分图的定义就可以了

• SGU - 172
• 解析

这道题只需要判断给出的数据是否合法，且数据完美地分为X部（考试）、Y部（学生），因此就是一个标准的非连通图二分图判断。

考试与学生的关系可以看做连线，这样我们就得到了一个图，其实是多个图。可以通过遍历每一个没有标记的点来判别每一个连通图是否都是二分图，只要有一个不是，就判断"no"。这里作者用vector 的邻接表储存图，col[] 储存标记。

这里的方案其实就是X、Y部中的某一部。(⊙_⊙)

• 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
int n_cla,n_stu,col[30005],error;
vector<int> vec[30005];
vector<int> ans;
void Solve(int u,int c)
{
	col[u]=c;
	if(c%2) ans.push_back(u);
	for(int i=0;i<(int)vec[u].size();i++)
	{
		int v=vec[u][i];
		if(col[v]){if((c+1)%2!=col[v]%2)error=true;continue;}
		Solve(v,c+1);
		if(error) return;
	}
}
int main()
{
	scanf("%d%d",&n_cla,&n_stu);
	for(int i=1;i<=n_stu;i++)
	{
		int A,B;scanf("%d%d",&A,&B);
		vec[B].push_back(A);vec[A].push_back(B);
	}
	for(int i=1;i<=n_cla;i++)
		if(!col[i])
		{
			Solve(i,1);
			if(error)
			{
				puts("no");
				return 0;
			}
		}
	printf("yes\n%d\n%d",ans.size(),ans[0]);
	for(int i=1;i<(int)ans.size();i++)
		printf(" %d",ans[i]);
	return 0;
}

◆最大匹配◆ The Perfect Stall

把匈牙利算法的板套上去

• POJ - 1274
• 解析

1. 图的建立

虽然二分图分为2个部（牛栏、奶牛），但实际上它还是一个图——所以必须将2个部的点放入同一个图中。这里可以通过将牛放入1~N的点，把牛栏放入N+1~N+M的点中。

2. 匈牙利算法的实现

寻找增广路径一般是采用DFS：

bool DFS(int u)
{
	for(int i=0;i<(int)vec[u].size();i++) //枚举邻接点
	{
		int v=vec[u][i];
		if(vis[v]) continue; //之前没有访问
		vis[v]=true; //标记
		if(mat[v]==0 || DFS(mat[v])) //如果该点没有匹配，或通过该点能向下找到一个未匹配点
		{ //这就是一条增广路径
			mat[u]=v;mat[v]=u; //反边
			return true;
		}
	}
	return false;
}

这道题比较基础，只要求找到最大匹配的数量，因此直接使用匈牙利算法，统计有多少组匹配就可以了。

• 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 200
int n,m,mat[2*MAXN+5];
bool vis[2*MAXN+5];
vector<int> vec[2*MAXN+5];
bool DFS(int u)
{
	for(int i=0;i<(int)vec[u].size();i++)
	{
		int v=vec[u][i];
		if(vis[v]) continue;
		vis[v]=true;
		if(mat[v]==0 || DFS(mat[v]))
		{
			mat[u]=v;mat[v]=u;
			return true;
		}
	}
	return false;
}
int Solve()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(vis,false,sizeof vis);
		if(mat[i]==0 && DFS(i))
			ans++;
	}
	return ans;
}
int main()
{
	while(scanf("%d%d",&n,&m)==2)
	{
		memset(mat,0,sizeof mat);
		for(int i=1;i<=n;i++)
		{
			int n_;scanf("%d",&n_);
			for(int j=0,x;j<n_;j++)
			{
				scanf("%d",&x);
				vec[i].push_back(x+n);
				vec[x+n].push_back(i);
			}
		}
		printf("%d\n",Solve());
		for(int i=1;i<=n;i++) vec[i].erase(vec[i].begin(),vec[i].end());
		for(int i=1;i<=m;i++) vec[i+n].erase(vec[i+n].begin(),vec[i+n].end());
	}
	return 0;
}

◆最小覆盖◆ Machine Schedule

就像一道结论题，结论一发现，就没什么难点了

• POJ - 1325
• 解析

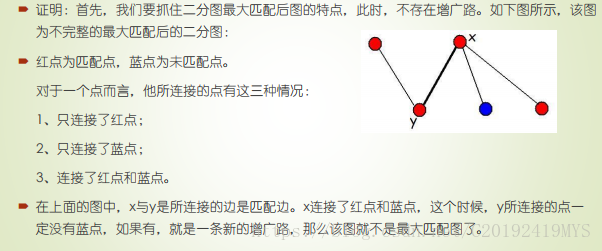
1. König定理

最小覆盖点数=最大匹配数

下面是证明：





2. 所以这道题还是最大匹配~

• 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 200
int n,m,mat[2*MAXN+5];
bool vis[2*MAXN+5];
vector<int> vec[2*MAXN+5];
bool DFS(int u)
{
	for(int i=0;i<(int)vec[u].size();i++)
	{
		int v=vec[u][i];
		if(vis[v]) continue;
		vis[v]=true;
		if(mat[v]==0 || DFS(mat[v]))
		{
			mat[u]=v;mat[v]=u;
			return true;
		}
	}
	return false;
}
int Solve()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(vis,false,sizeof vis);
		if(mat[i]==0 && DFS(i))
			ans++;
	}
	return ans;
}
int main()
{
	while(scanf("%d%d",&n,&m)==2)
	{
		memset(mat,0,sizeof mat);
		for(int i=1;i<=n;i++)
		{
			int n_;scanf("%d",&n_);
			for(int j=0,x;j<n_;j++)
			{
				scanf("%d",&x);
				vec[i].push_back(x+n);
				vec[x+n].push_back(i);
			}
		}
		printf("%d\n",Solve());
		for(int i=1;i<=n;i++) vec[i].erase(vec[i].begin(),vec[i].end());
		for(int i=1;i<=m;i++) vec[i+n].erase(vec[i+n].begin(),vec[i+n].end());
	}
	return 0;
}

---

The End

Thanks for reading!

- Lucky_Glass