奇异值分解(SVD) --- 几何意义 （转载）

PS：一直以来对SVD分解似懂非懂，此文为译文，原文以细致的分析+大量的可视化图形演示了SVD的几何意义。能在有限的篇幅把 这个问题讲解的如此清晰，实属不易。原文举了一个简单的图像处理问题，简单形象，真心希望路过的各路朋友能从不同的角度阐述下自己对SVD实际意义的理 解，比如 个性化推荐中应用了SVD，文本以及Web挖掘的时候也经常会用到SVD。

原文：We recommend a singular value decomposition

关于线性变换部分的一些知识可以猛戳这里  奇异值分解(SVD) --- 线性变换几何意义

奇异值分解( The singular value decomposition )

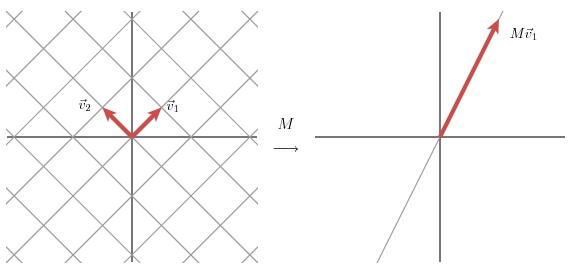
该部分是从几何层面上去理解二维的SVD：对于任意的 2 x 2 矩阵，通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。

我们可以通过向量的方式来描述这个事实: 首先，选择两个相互正交的单位向量 v₁ 和 v₂, 向量Mv₁ 和 Mv₂ 正交。

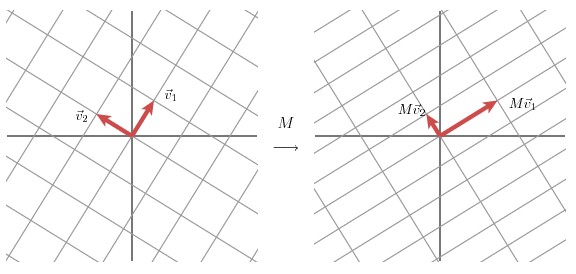
u₁ 和 u₂分别表示Mv₁ 和 Mv₂的单位向量，σ₁ * u₁ =  Mv₁ 和 σ₂ * u₂ =  Mv₂。σ₁ 和 σ₂分别表示这不同方向向量上的模，也称作为矩阵 M 的奇异值。

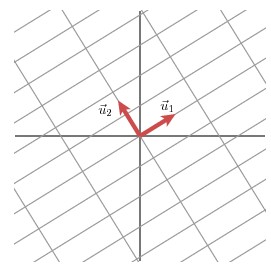
这样我们就有了如下关系式

Mv₁ = σ₁u₁ 
Mv₂ = σ₂u₂

我们现在可以简单描述下经过 M 线性变换后的向量 x 的表达形式。由于向量v₁ 和 v₂是正交的单位向量，我们可以得到如下式子：

x = (v₁x) v₁ + (v₂x) v₂

这就意味着：

Mx = (v₁x) Mv₁ + (v₂x) Mv₂ 
Mx = (v₁x) σ₁u₁ + (v₂x) σ₂u₂

向量内积可以用向量的转置来表示，如下所示

vx = v^Tx

最终的式子为

Mx = u₁σ₁ v₁^Tx + u₂σ₂ v₂^Tx 
M = u₁σ₁ v₁^T + u₂σ₂ v₂^T

上述的式子经常表示成

M = UΣV^T

u 矩阵的列向量分别是u₁,u₂ ，Σ 是一个对角矩阵，对角元素分别是对应的σ₁ 和 σ₂，V 矩阵的列向量分别是v₁,v₂。上角标 T 表示矩阵 V 的转置。

这就表明任意的矩阵 M 是可以分解成三个矩阵。V 表示了原始域的标准正交基，u 表示经过 M 变换后的co-domain的标准正交基，Σ 表示了V 中的向量与u 中 相对应向量之间的关系。(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)

如何获得奇异值分解？( How do we find the singular decomposition? )

事实上我们可以找到任何矩阵的奇异值分解，那么我们是如何做到的呢？假设在原始域中有一个单位圆，如下图所示。经过 M 矩阵变换以后在co-domain中单位圆会变成一个椭圆，它的长轴(Mv₁)和短轴(Mv₂)分别对应转换后的两个标准正交向量，也是在椭圆范围内最长和最短的两个向量。

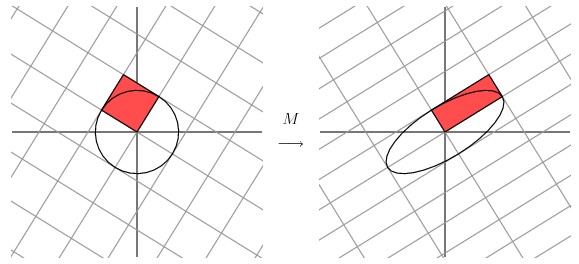
换句话说，定义在单位圆上的函数|Mx|分别在v₁和v₂方向上取得最大和最小值。这样我们就把寻找矩阵的奇异值分解过程缩小到了优化函数|Mx|上了。结果发现（具体的推到过程这里就不详细介绍了）这个函数取得最优值的向量分别是矩阵 MT M 的特征向量。由于MTM是对称矩阵，因此不同特征值对应的特征向量都是互相正交的，我们用vi 表示MTM的所有特征向量。奇异值σ_i = |Mv_i| ， 向量 u_i 为 Mv_i 方向上的单位向量。但为什么u_i也是正交的呢？

推倒如下：

σ_i 和 σ_j分别是不同两个奇异值

Mv_i = σ_iu_i 
Mv_j = σ_ju_j.

我们先看下Mv_iMv_j，并假设它们分别对应的奇异值都不为零。一方面这个表达的值为0，推到如下

Mv_i Mv_j = v_i^TM^T Mv_j = v_i M^TMv_j = λ_jv_i v_j = 0

另一方面，我们有

Mv_i Mv_j = σ_iσ_j u_i u_j = 0

因此，u_i 和 u_j是正交的。但实际上，这并非是求解奇异值的方法，效率会非常低。这里也主要不是讨论如何求解奇异值，为了演示方便，采用的都是二阶矩阵。

应用实例(Another example)

现在我们来看几个实例。

实例一

经过这个矩阵变换后的效果如下图所示

在这个例子中，第二个奇异值为 0，因此经过变换后只有一个方向上有表达。

M = u₁σ₁ v₁^T.

换句话说，如果某些奇异值非常小的话，其相对应的几项就可以不同出现在矩阵 M 的分解式中。因此，我们可以看到矩阵 M 的秩的大小等于非零奇异值的个数。

实例二

我们来看一个奇异值分解在数据表达上的应用。假设我们有如下的一张 15 x 25 的图像数据。

如图所示，该图像主要由下面三部分构成。

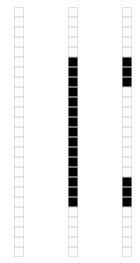
我们将图像表示成 15 x 25 的矩阵，矩阵的元素对应着图像的不同像素，如果像素是白色的话，就取 1，黑色的就取 0. 我们得到了一个具有375个元素的矩阵，如下图所示

如果我们对矩阵M进行奇异值分解以后，得到奇异值分别是

σ₁ = 14.72 
σ₂ = 5.22 
σ₃ = 3.31

矩阵M就可以表示成

M=u₁σ₁ v₁^T + u₂σ₂ v₂^T + u₃σ₃ v₃^T

v_i具有15个元素，u_i 具有25个元素，σ_i 对应不同的奇异值。如上图所示，我们就可以用123个元素来表示具有375个元素的图像数据了。

实例三

减噪(noise reduction)

前面的例子的奇异值都不为零，或者都还算比较大，下面我们来探索一下拥有零或者非常小的奇异值的情况。通常来讲，大的奇异值对应的部分会包含更多的信息。比如，我们有一张扫描的，带有噪声的图像，如下图所示

我们采用跟实例二相同的处理方式处理该扫描图像。得到图像矩阵的奇异值：

σ₁ = 14.15 
σ₂ = 4.67 
σ₃ = 3.00 
σ₄ = 0.21 
σ₅ = 0.19 
... 
σ₁₅ = 0.05

很明显，前面三个奇异值远远比后面的奇异值要大，这样矩阵 M 的分解方式就可以如下：

M 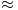 u₁σ₁ v₁^T + u₂σ₂ v₂^T + u₃σ₃ v₃^T

经过奇异值分解后，我们得到了一张降噪后的图像。

实例四

数据分析(data analysis)

我们搜集的数据中总是存在噪声：无论采用的设备多精密，方法有多好，总是会存在一些误差的。如果你们还记得上文提到的，大的奇异值对应了矩阵中的主要信息的话，运用SVD进行数据分析，提取其中的主要部分的话，还是相当合理的。

作为例子，假如我们搜集的数据如下所示：

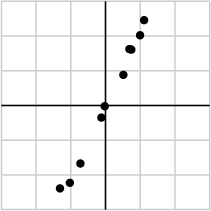
我们将数据用矩阵的形式表示：

经过奇异值分解后，得到

σ₁ = 6.04 
σ₂ = 0.22

由于第一个奇异值远比第二个要大，数据中有包含一些噪声，第二个奇异值在原始矩阵分解相对应的部分可以忽略。经过SVD分解后，保留了主要样本点如图所示

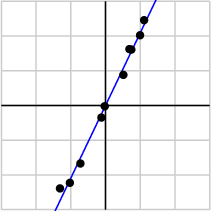
就保留主要样本数据来看，该过程跟PCA( principal component analysis)技术有一些联系，PCA也使用了SVD去检测数据间依赖和冗余信息.

总结(Summary)

这篇文章非常的清晰的讲解了SVD的几何意义，不仅从数学的角度，还联系了几个应用实例形象的论述了SVD是如何发现数据中主要信息的。在 netflix prize中许多团队都运用了矩阵分解的技术，该技术就来源于SVD的分解思想，矩阵分解算是SVD的变形，但思想还是一致的。之前算是能够运用矩阵分解 技术于个性化推荐系统中，但理解起来不够直观，阅读原文后醍醐灌顶，我想就从SVD能够发现数据中的主要信息的思路，就几个方面去思考下如何利用数据中所 蕴含的潜在关系去探索个性化推荐系统。也希望路过的各位大侠不吝分享呀。

References:

Gilbert Strang, Linear Algebra and Its Applications. Brooks Cole

William H. Press et al, Numercial Recipes in C: The Art of Scientific Computing. Cambridge University Press.

Dan Kalman, A Singularly Valuable Decomposition: The SVD of a Matrix, The College Mathematics Journal 27 (1996), 2-23.

If You Liked This, You're Sure to Love That, The New York Times, November 21, 2008.

http://blog.sciencenet.cn/blog-696950-699432.html