组合数们&&错排&&容斥原理

最近做了不少的组合数的题
这里简单总结一下下

1.n,m很大p很小 且p为素数
p要1e7以下的 可以接受On的时间和空间
然后预处理阶乘 Lucas定理来做
以下是代码

/*Hdu3037 Saving Beans*/
#include<cstdio>
#include<cstring>
#include<iostream>
#define ll long long
#define maxn 1000010
using namespace std;
ll T,n,m,p,f[maxn];
void Get(){
    f[]=;
    for(int i=;i<=p;i++)
        f[i]=f[i-]*i%p;
}
ll qm(ll a,ll b){
    a%=p;ll r=;
    while(b){
        if(b&)r=r*a%p;
        b>>=;a=a*a%p;
    }
    return r;
}
ll C(ll a,ll b){
    if(b>a)return ;
    return f[a]*qm(f[b]*f[a-b],p-)%p;
}
ll Lcs(ll a,ll b){
    if(b==)return ;
    return C(a%p,b%p)*Lcs(a/p,b/p)%p;
}
int main(){
    cin>>T;
    while(T--){
        cin>>n>>m>>p;Get();
        cout<<Lcs(n+m,n)<<endl;
    }
    return ;
}

2.n很大,m很小,p很大,且p为素数p>m

m很小我们可以直接暴力,保证了p大于m,也就是pm互质,保证存在逆元

/*[FZU 2020] 组合*/
#include<cstdio>
#include<cstring>
#include<iostream>
#define ll long long
#define maxn 1000010
using namespace std;
ll T,n,m,p;
ll qm(ll a,ll b){
    a%=p;ll r=;
    while(b){
        if(b&)r=r*a%p;
        b>>=;a=a*a%p;
    }
    return r;
}
ll C(ll a,ll b){
    if(b>a)return ;ll res=;
    for(ll i=a,j=;j<=b;i--,j++){
        res*=i%p;res%=p;res*=qm(j,p-);res%=p;
    }
    return res;
}
int main(){
    cin>>T;
    while(T--){
        cin>>n>>m>>p;
        cout<<C(n,m)<<endl;
    }
    return ;
}

3.n很大,m很小,p很大,且p为素数

同上可用暴力,但是p虽然会prime但是可能m是p的倍数逆元可能不存在

所以我们用Lucas定理,把m分解成一个p进制数,保证比p小,就可以同上了

/*ZOJ 3557 How Many Sets II */
#include<cstdio>
#include<cstring>
#include<iostream>
#define ll long long
using namespace std;
ll T,n,m,p;
ll qm(ll a,ll b){
    a%=p;ll r=;
    while(b){
        if(b&)r=r*a%p;
        b>>=;a=a*a%p;
    }
    return r;
}
ll C(ll a,ll b){
    if(b>a)return ;ll res=;
    for(ll i=a,j=;j<=b;i--,j++){
        res*=i%p;res%=p;res*=qm(j,p-);res%=p;
    }
    return res;
}
ll Lcs(ll a,ll b){
    if(b==)return ;
    return C(a%p,b%p)*Lcs(a/p,b/p)%p;
}

int main(){
    while(cin>>n>>m>>p)
        cout<<Lcs(n-m+,m)<<endl;
    return ;
}

下面是几个性质

1.C(n,0),C(n,1),,,,,C(n,n)里面奇数的个数

= 2^(n二进制表示下的1的个数)  (好像有组合数的做法,这个是打表找的规律)

2.

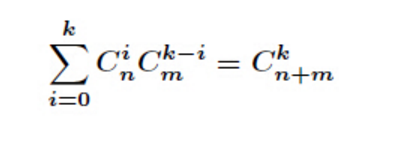
范德莫恒等式

错排问题&&容斥原理

Ai表示i在i位置的序列个数,显然 Ai=(n-1)!  Ai∩Aj=(n-2)!

Ai的反也就是i不在i位置的序列个数,

所以A1反∩A2反∩.....∩An反 = ( A1∪A2∪....∪An )反=U- ( A1∪A2∪....∪An )

U=n!,所以ans=n!-C(n,1)*(n-1)!+C(n,2)*(n-2)!......

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#define ll long long
using namespace std;
int n;ll f[],ans;
int main(){
    f[]=;for(int i=;i<=;i++)f[i]=f[i-]*i;
    while(~scanf("%d",&n)){
        ans=f[n];for(int i=;i<=n;i++)
            if(i&)ans-=f[n]/f[i];
            else ans+=f[n]/f[i];
        printf("%lld\n",ans);
    }
    return ;
}

这个是比较裸地,然后我们看一个题目

HDU 2068

题意:满足a[i]=i的个数一般或以上的序列个数

我们就枚举有x个a[i]=i,然后剩下的就是n-x错排了 乘法原理乘一下

高中用的为数不多的组合数的题目就是隔板法,还有一种模型就是解的个数

x1+x2+x3....+xm=n   问合法的x1x2x3....个数,若保证是正整数就是C(n-1,m-1),可能为0 那就每个x都加一 右边变成n+m,答案就是C(n+m-1,m-1)

看这样一道题 HDU6397

题意:x1+x2+x3....+xm=k  0<=xi<=n

先不管<=n这个条件,我们先转化成正整数:x1+x2+x3....+xm=k+m

考虑<=n这件事: 我们能求出来的是没有上界的模型,倘若我们知道只有x1>n,那我们用x1-n替换x1,就把这个变成了我们可以解决的模型(注意右边-n)

然后就可以想到容斥原理,就是看有几个xi>n,我们剪掉一个x大于n的时候会多剪掉两个的,就是简单的+-+-的容斥模型了

然后注意特殊的数据

#include<cstdio>
#define ll long long
using namespace std;
int T,n,m,k;
const ll mod=;
ll ans,f[],inv[];
void extgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){
        d=a;x=;y=;
    }
    else{
        extgcd(b,a%b,d,y,x);
        y-=x*(a/b);
    }
}
ll inverse(ll a,ll n){
    ll d,x,y;
    extgcd(a,n,d,x,y);
    return d==?(x+n)%n:;
}
ll C(int x,int y){
    return f[x]*inv[y]%mod*inv[x-y]%mod;
}
int main(){

    scanf("%d",&T);f[]=;inv[]=;
    for(int i=;i<=;i++){
        f[i]=f[i-]*i%mod;
        inv[i]=inverse(f[i],mod);
    }
    while(T--){
        scanf("%d%d%d",&n,&m,&k);
        if((n-)*(ll)m<k){
            printf("0\n");continue;
        }
        int x=k-+m,y=m-;ans=;f[]=;
        for(int i=;i<=m&&x>=y;i++,x-=n){
            if(i&)ans+=C(m,i-)*C(x,y)%mod;
            else ans-=C(m,i-)*C(x,y)%mod;
            ans+=mod;ans%=mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}

再看个稍微麻烦一点的

cf451E

题意同上,只不过上界不是固定的n,是一个ai

乍一看好像挺难得因为上面的状态的是   几个不合法的,  而现在是  哪几个不合法的

不过好在m很小,我们可以利用状丫确定状态,然后容斥的时候就不能 x个不合法的一起算了

而是奇数个不合法的话,就对答案贡献为-,偶数为正.

#include<iostream>
#define ll long long
using namespace std;
const ll mod=;
int n,cnt;
ll f[],ans,s,k;
void extgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){
        d=a;x=;y=;
    }
    else{
        extgcd(b,a%b,d,y,x);
        y-=x*(a/b);
    }
}
ll inverse(ll a,ll n){
    ll d,x,y;
    extgcd(a,n,d,x,y);
    return d==?(x+n)%n:;
}
ll C(ll x,ll y){
    ll res=;
    for(ll i=x,j=;j<=y;i--,j++){
        res*=i%mod;res%=mod;res*=inverse(j,mod);res%=mod;
    }
    return res;
}
int main(){
    cin>>n>>s;
    for(int i=;i<=n;i++)
        cin>>f[i];
    for(int S=;S<(<<n);S++){
        cnt=;k=s;
        for(int j=;j<=n;j++)
            if(S&(<<j-)){
                cnt++;k-=f[j]+;
            }
        if(k<)continue;
        if(cnt&)ans-=C(k+n-,n-);
        else ans+=C(k+n-,n-);
        ans+=mod;ans%=mod;
    }
    cout<<ans<<endl;
    return ;
}

然后是一个比较emmmmm好像也不是很简单的容斥原理

UVAlive 5846

题意:一个圈上有很多点,两两连边,每条边是红/蓝,然后问形成的同色三角形的个数

ans=总三角形的个数-异色三角形的个数

tot=C(n,3),下面考虑异色三角形个数

以为只有两种颜色,所以异色三角形的构成是112或者 122

也就是说,有两个顶点连出去的边异色,我们转而研究点,对于每个点,选两条异色边,就一定构成一个异色三角形

然后每个三角形统计了两边,在/2就好了

#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 1010
using namespace std;
int T,n,a[maxn],b[maxn];
long long ans;
int main(){
    scanf("%d",&T);
    while(T--){
        memset(a,,sizeof(a));
        memset(b,,sizeof(b));
        scanf("%d",&n);int x;ans=;
        for(int i=;i<n;i++)
            for(int j=;j<=n-i;j++){
                scanf("%d",&x);
                if(x)a[i]++,a[i+j]++;
                else b[i]++,b[i+j]++;
            }
        for(int i=;i<=n;i++)
            ans-=a[i]*b[i];
        ans/=;ans+=(long long)n*(n-)*(n-)/;
        printf("%lld\n",ans);
    }
    return ;
}