[Bzoj1767][Ceoi2009]harbingers （树上斜率优化）

1767: [Ceoi2009]harbingers

---

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 451  Solved: 120
[Submit][Status][Discuss]

Description

---

给定一颗树，树中每个结点有一个邮递员，每个邮递员要沿着唯一的路径走向capital(1号结点)，每到一个城市他可以有两种选择： 1.继续走到下个城市 2.让这个城市的邮递员替他出发。 每个邮递员出发需要一个准备时间W[I]，他们的速度是V[I]，表示走一公里需要多少分钟。 现在要你求出每个城市的邮递员到capital的最少时间(不一定是他自己到capital，可以是别人帮他） N<=100000 3 ≤ N ≤ 100 000 0 ≤ Si≤ 10^9 1 ≤ Vi≤ 10^9 The length of each road will not exceed 10 000 For 20% of the tests, N ≤ 2 500 For 50% of the tests, each town will have at most 2 adjacent roads (i.e., the graph of roads will be a line)

Input

---

N 以下N-1行A,B,C三个数表示A,B之间有一条长为C的边。 再N行每行两数Wi,Vi

Output

---

  输出有一行N-1个数表示如题所述。

Sample Input

---

Sample Output

---

HINT

---

分析：

---

考虑暴力

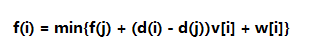其中j为i的祖先。

发现很显然的斜率优化式子模型，转化成点斜式

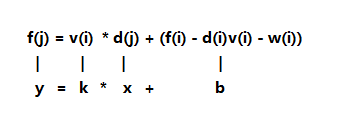
发现x是单增的，可以使用单调栈维护下凸包，答案就是使截矩b最小的点对（x，y）

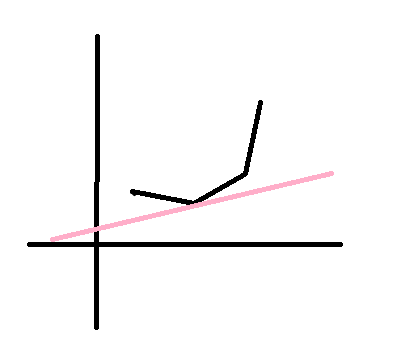
但发现斜率k是不单调的，代表决策不单调，所以只有采用二分寻找最优决策。

这还是很显然的，但是这道题是在树上，树上根节点到当前点的凸包要在它每个儿子都会使用到，要想办法维护根节点到每个点的凸包。

我们加入一个点后，不从队首开始pop，而是二分寻找它该加入的位置，把那个位置改成当前点，并记录下原来的点和位置。

处理它的所有儿子结点后，又把当前点改回原来的点。这样就做到保存各点凸包信息了。

坑点：会炸long long  比较斜率的时候被迫使用double。

AC代码：

---

# include <iostream>
# include <cstdio>
# include <cstring>
using namespace std;
const int N = 3e5 + ;
typedef long long LL;
int n,dt,head[N],que[N];LL f[N],d[N],v[N],w[N];
struct Edge{
    int to,nex;LL w;
}edge[N << ];
void AddEdge(int u,int v,LL w)
{
    edge[++dt] = (Edge){v,head[u],w};
    head[u] = dt;
}
LL x(int i){return d[i];}
LL y(int i){return f[i];}
LL Get(int A,int B){return f[A] + (d[B] - d[A]) * v[B] + w[B];}
double slope(int A,int B){return ((double)(y(B) - y(A))) / ((double)(x(B) - x(A)));}
bool Cross(int A,int B,int C){return slope(B,C) <= slope(A,B);}
int find(int x,int tp)
{
    int l = ,r = tp,ret = ,mid;
    while(l <= r)
    {
        mid = l + r >> ;
        if(Get(que[mid],x) < Get(que[mid - ],x))ret = mid,l = mid + ;
        else r = mid - ;
    }
    return ret;
}
int Find(int z,int tp)
{
    int l = ,r = tp,ret = tp + ,mid;
    while(l <= r)
    {
        mid = l + r >> ;
        if(Cross(que[mid - ],que[mid],z))ret = mid,r = mid - ;
        else l = mid + ;
    }
    return ret;
}
void dfs(int u,int pos,int fa)
{
    int qpos,qtop;
    f[u] = Get(que[find(u,pos)],u);
    qpos = Find(u,pos);qtop = que[qpos];
    que[qpos] = u;
    for(int i = head[u];i;i = edge[i].nex)
    {
        if(edge[i].to == fa)continue;
        d[edge[i].to] = d[u] + edge[i].w;
        dfs(edge[i].to,qpos,u);
    }
    que[qpos] = qtop;
}
int main(){
   scanf("%d",&n);
   int x,y,z;
   for(int i = ;i < n;i++)
   {
       scanf("%d %d %d",&x,&y,&z);
       AddEdge(x,y,z);AddEdge(y,x,z);
   }
   for(int i = ;i <= n;i++)scanf("%lld %lld",&w[i],&v[i]);
   dfs(,,);printf("%lld",f[]);
   for(int i = ;i <= n;i++)printf(" %lld",f[i]);
}