Scaling with Microservices and Vertical Decomposition – dev.otto.de https://dev.otto.de/2014/07/29/scaling-with-microservices-and-vertical-decomposition/

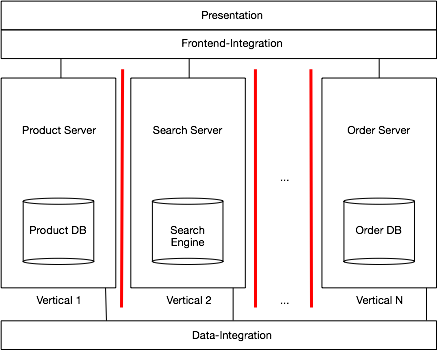
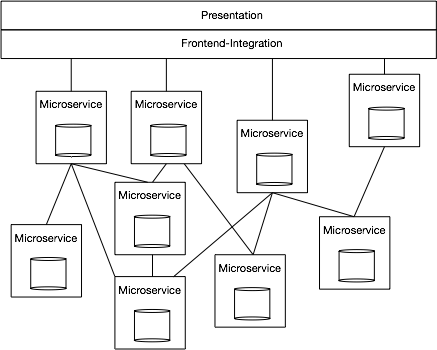
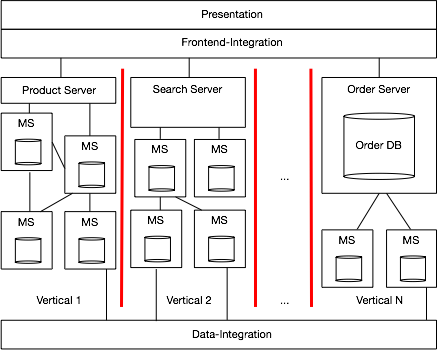
Scaling with Microservices and Vertical Decomposition的更多相关文章

  1. HTML5资料

    1 Canvas教程 <canvas>是一个新的用于通过脚本(通常是JavaScript)绘图的HTML元素.例如,他可以用于绘图.制作图片的组合或者简单的动画(当然并不那么简单).It ...

  2. Video for Linux Two API Specification revision0.24【转】

    转自:http://blog.csdn.net/jmq_0000/article/details/7536805#t136 Video for Linux Two API Specification ...

  3. 什么是微服务 Martin Fowler的microservices

    https://martinfowler.com/articles/microservices.html https://martinfowler.com/microservices/ 微服务,最早由 ...

  4. Microservices

    Microservices What are Microservices? What are Microservices - microservices.io Microservices - mart ...

  5. A Brief History of Scaling LinkedIn

    原文地址 LinkedIn started in 2003 with the goal of connecting to your network for better job opportuniti ...

  6. We Recommend a Singular Value Decomposition

    We Recommend a Singular Value Decomposition Introduction The topic of this article, the singular val ...

  7. [转载]We Recommend a Singular Value Decomposition

    原文:http://www.ams.org/samplings/feature-column/fcarc-svd Introduction The topic of this article, the ...

  8. Securing Spring Cloud Microservices With OAuth2

    From Zero to OAuth2 in Spring cloud Today I am presenting hours of research about a (apparently) sim ...

  9. 131.006 Unsupervised Learning - Feature Scaling | 非监督学习 - 特征缩放

    @(131 - Machine Learning | 机器学习) 1 Feature Scaling transforms features to have range [0,1] according ...

随机推荐

  1. iOS阴影

    但是如果把masksToBounds设置为yes就没有阴影了     UIButton *view = [[UIButton alloc]initWithFrame:CGRectMake(, , ,  ...

  2. 【Luogu】P1306斐波那契公约数（递推）

    题目链接 有个定理叫gcd(f(n),f(m))=f(gcd(n,m)) 所以递推就好了. #include<cstdio> #include<cstdlib> #includ ...

  3. SPOJ CIRU The area of the union of circles ——Simpson积分

    [题目分析] 圆的面积并. 直接Simpson积分,(但是有计算几何的解法,留着flag). simpson积分,如果圆出现了不连续的情况,是很容易出事情的.(脑补一下) 但是没有什么办法,本来就是一 ...

  4. 酒厂选址（codevs 1507）

    题目描述 Description Abstinence(戒酒)岛的居民们酷爱一种无酒精啤酒.以前这种啤酒都是从波兰进口,但今年居民们想建一个自己的啤酒厂.岛上所有的城市都坐落在海边,并且由一条沿海岸线 ...

  5. angular中多控制器的依赖注入写法

    直接看图,每个控制器有自己的名称,第二个参数中有需要注入的依赖对象,最后是我们的自定义函数,这样我们可以以模块化的方式进行书写.

  6. HDU 4474 Yet Another Multiple Problem【2012成都regional K题】 【BFS+一个判断技巧】

    Yet Another Multiple Problem Time Limit: 40000/20000 MS (Java/Others)    Memory Limit: 65536/65536 K ...

  7. perl学习之精髓中的精髓

    1.是函数就有返回值: 比如:chomp函数,其可以除去换行符,但其也有返回值 chomp($xx) #这是去除xx的换行符 $yy=chomp($xx)  #这是看这次除去了几个换行符,也就是函数运 ...

  8. Executors

    提供了工厂方法: Factory and utility methods for Executor, ExecutorService, ScheduledExecutorService, Thread ...

  9. tcp-time-wait-state

    https://vincent.bernat.im/en/blog/2014-tcp-time-wait-state-linux

  10. ios Crash Log 分析汇总

    方法一: 1.xcode 有自带的symbolicatecrash,可以将.crash文件中的16进制地址转换成可读的函数地址. symbolicatecrash位于: /Applications/X ...