LuoguP1314 聪明的质检员 【二分答案/前缀和】

美丽的题号预示着什么...

描述

小 T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有n个矿石，从1到n逐一编号，每个矿石都有自己的重量wi以及价值vi。检验矿产的流程是：
1、给定m个区间[Li，Ri]；
2、选出一个参数W；
3、对于一个区间[Li，Ri]，计算矿石在这个区间上的 检验值Yi：

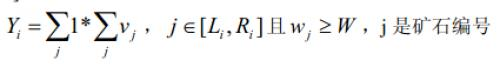
这批矿产的 检验结果Y 为各个区间的检验值之和 。即： Y1+Y2...+Ym
若这批矿产的 检验结果 与所给标准值S相差太多，就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产，所以他想通过调整参数W的值，让 检验结果 尽可能的靠近标准值S，即使得 S-Y 的绝对值最小。请你帮忙求出这个最小值。

格式

输入格式

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n行，每行2个整数，中间用空格隔开，第i+1行表示i号矿石的重量wi和价值vi 。

接下来的m行，表示区间，每行2个整数，中间用空格隔开，第i+n+1行表示区间[Li,Ri]的两个端点Li和Ri。 注意：不同区间可能重合或相互重叠。

输出格式

输出只有一行，包含一个整数，表示所求的最小值。

样例1

样例输入1

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3

样例输出1

10

提示

样例说明：当W选4的时候，三个区间上检验值分别为20、5、0，这批矿产的检验结果为25，此时与标准值S相差最小为10。

对于10%的数据，有1 ≤ n，m ≤ 10；
对于30%的数据，有1 ≤ n，m ≤ 500；
对于50%的数据，有1 ≤ n，m ≤ 5,000；
对于70%的数据，有1 ≤ n，m ≤ 10,000；
对于100%的数据，有1 ≤ n，m ≤ 200,000，0 < wi, vi ≤ 10^6，0 < S ≤ 10^12，1 ≤ Li ≤ Ri ≤ n。

来源

NOIp2011提高组Day2第二题

这道题...题面读了好久（晦涩难懂）

做背包做惯了于是以下及我的代码把数组v与w的意义调换了一下（v为重量，w为价值）

因为参数值W是不固定的，而且坐落在有序的一段区间上（1~max v[i] ），所以我们可以愉快地使用二分答案。

如果我们二分出的这个参数值使得Y较小，说明参数取得有些大，满足的值很少，我们向左移一移。

如果我们二分出的这个参数值使得Y较大，说明参数取得有些小，满足的值很多，我们向右移一移。

根据lyd老师的指引，我们愉快地写出了二分答案的代码

    int l=,r=mx;
    while(l<r)
    {
        int mid=(l+r+)>>;
        Y=check(mid);
        if(Y<s) r=mid-;
        else l=mid;
        ans=min(ans,abs(s-Y));
    }

接下来就是check函数的写法。

由于数据达到了1e6，我们肯定不能暴力计算区间和，前缀和坠吼了。

ll check(int x)
{
    ll tmp=;
    for(int i=;i<=n;i++)
    {
        sum[i]=sum[i-];
        cnt[i]=cnt[i-];
        if(v[i]>=x)
        {
            sum[i]+=w[i];
            cnt[i]++;
        }
    }
    for(int i=;i<=m;i++)
     tmp+=(sum[q[i].second]-sum[q[i].first-])*(cnt[q[i].second]-cnt[q[i].first-]);
    return tmp;
}

于是我们就愉快地AC了。

code

 #include<cstdio>
 #include<algorithm>
 #include<utility>
 #define inf (1LL<<60)

 using namespace std;
 typedef long long ll;

 int n,m,mx;
 int v[],w[];
 ll ans=inf,s,Y,sum[],cnt[];
 pair<int,int> q[];
 /*ll check(int x)
 {
     ll tmp=0;
     for(int i=1;i<=m;i++)
     {
         int pos=lower_bound(v+1,v+n+1,x)-v;
         if(pos>q[i].second) continue;
         int cnt=max(pos,q[i].first);
         tmp+=(w[q[i].second]-w[cnt-1])*(q[i].second-cnt+1);
     }
     return tmp;
 }*/
 ll check(int x)
 {
     ll tmp=;
     for(int i=;i<=n;i++)
     {
         sum[i]=sum[i-];
         cnt[i]=cnt[i-];
         if(v[i]>=x)
         {
             sum[i]+=w[i];
             cnt[i]++;
         }
     }
     for(int i=;i<=m;i++)
      tmp+=(sum[q[i].second]-sum[q[i].first-])*(cnt[q[i].second]-cnt[q[i].first-]);
     return tmp;
 }
 int main()
 {
     scanf("%d%d%lld",&n,&m,&s);
     for(int i=;i<=n;i++)
      scanf("%d%d",&v[i],&w[i]),mx=max(mx,v[i]);
     for(int i=;i<=m;i++)
      scanf("%d%d",&q[i].first,&q[i].second);
 /*    sort(a+1,a+n+1,cmp);*/
 /*    sum[1]=a[1].w;
     for(int i=2;i<=n;i++)
      sum[i]=sum[i-1]+a[i].w;*/

     int l=,r=mx;
     while(l<r)
     {
         int mid=(l+r+)>>;
         Y=check(mid);
         if(Y<s) r=mid-;
         else l=mid;
         ans=min(ans,abs(s-Y));
     }
     printf("%lld",ans);
     return ;
 }

几个注意事项

§ 虽说没有负数的情况，但是ans初值本身开始也要赋得很大，否则会输出0. （因为这调了很久qaq），ans是long long类型，怎么赋初值？hzwer大神给了一个不错的写法

#define inf (1LL<<60)

§ 开始想排一遍序，然后前缀和直接调用就好了。然而...并没有注意到还有区间下标的限制，还是老实做吧orz！