笔记 Bioinformatics Algorithms Chapter7

一、Lloyd算法

算法1 Lloyd Algorithm  k_mean clustering
* Centers to Clusters: After centers have been selected, assign each data point to the cluster corresponding to its nearest center; ties are broken arbitrarily.
* Clusters to Centers: After data points have been assigned to clusters, assign each cluster’s center of gravity to be the cluster’s new center.

二、Soft-Kmeans 聚类

• Lloyd算法的缺点是对每个数据做出是或者非的决定；一种soft-kmean聚类方法对每个点属于哪一类，用一个评分体系来衡量

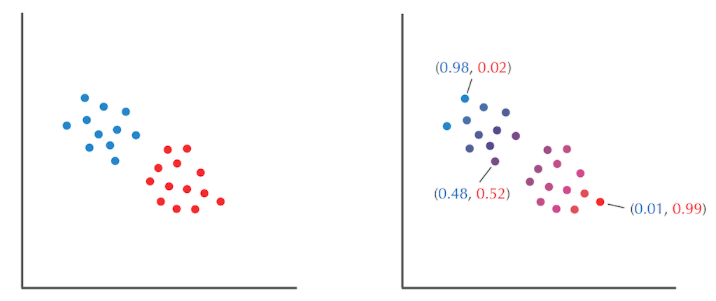
（1）条件概率

掷两个不知道bias的骰子，你要通过五组骰子掷出的结果来判断每次掷的是哪种骰子

　　五组实验，掷出 head的频率

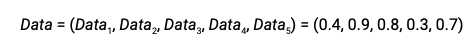
由估计出的骰子的分种，来计算每种骰子的bias，其中HiddenVector是一个用于对每种骰子分类的向量，筛子为A，值为1；骰子为B，值为0

用向量表示

上面是一个知道骰子的属性，计算每个骰子的bias

下面讲述知道每个骰子的bias，根据一组数据知道骰子的属性：

思路是：例如某次实验数据是掷出7个head，3个back，并且知道biasA是0.6，biasB是0.82

那么

由实验结果和bias得出A的几率更大，这次数据是由A骰子掷出的

利用条件概率的符号表示，那就是  Pr(Data_i|θ_A) > Pr(Data_i|θ_B)

（2）提出问题

我们可以由数据和参数（bias）推出HiddenVector

也可以以由数据和HiddenVector推出参数bias

那么，如果HiddenVector和参数（bias）都不知道怎么办

这个问题可以描述如下

（3）类似于Lloyd算法，我们可以随机选取初始的参数（bias），算出HiddenVector，然后利用HiddenVector算出参数，如此循环

(Data, ?, Parameters) → (Data, HiddenVector, Parameters)
                   → (Data, HiddenVector, ?)
                   → (Data, HiddenVector, Parameters')
                   → (Data, ?, Parameters')
                   → (Data, HiddenVector', Parameters')
                   →                  ...           

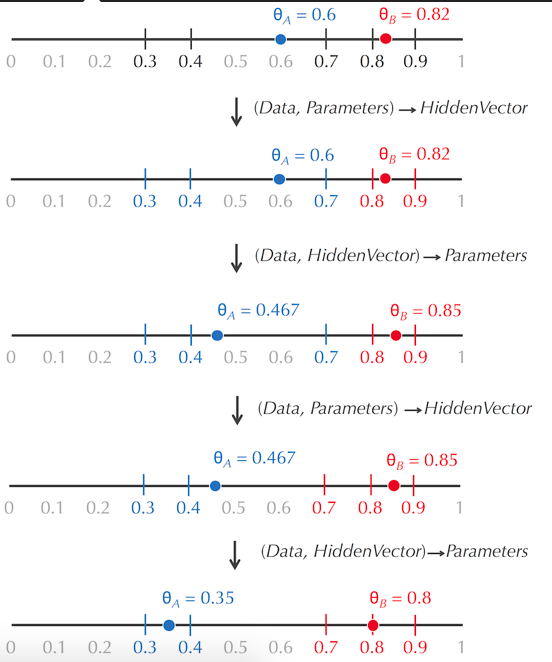
但是，对每个数据武断地认定用的是A还是B骰子是不好的，对于HiddenVector，可以将其转变为HiddenMatrix，其中在一列中，每个数是该条件概率的占比

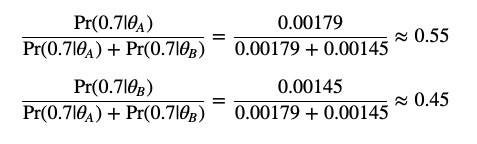
计算参数（bias）的过程也可以推导为

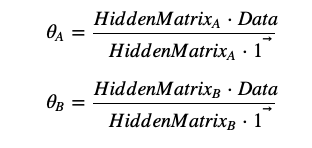
（4）The expectation maximization algorithm

对于一般的聚类问题，HiddenMatrix的计算就难以使用条件概率的占比，

HiddenMatrix每一列的值，其实是对每个数据点属于哪一类进行打分那么，当然是离某一个Center越近，这个打分应该越高

• 牛顿打分法：将每个Center看成恒星，数据看成行星，那么当然是离恒星越近，引力越大，利用Newtonian inverse-square law of gravitation打分：

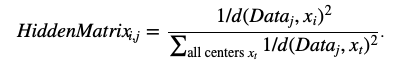
• 利用统计物理学的打分方法效果更好

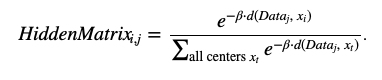
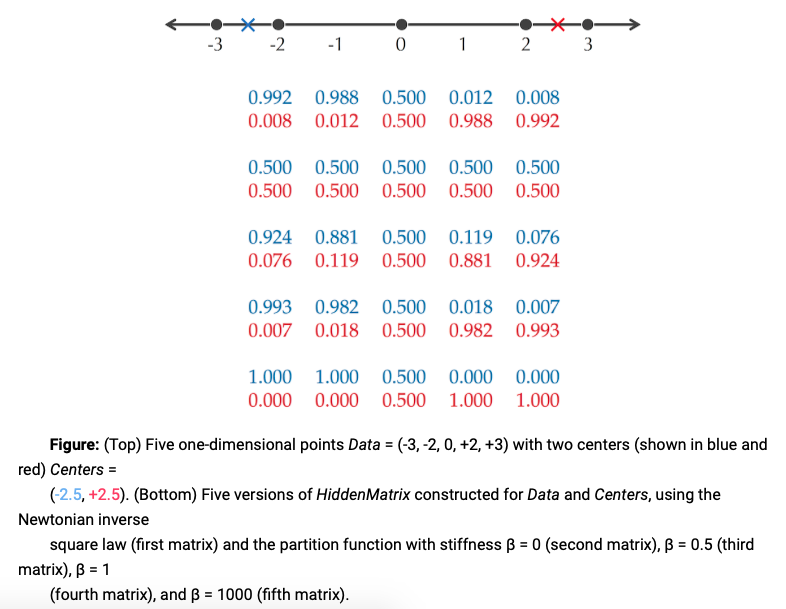
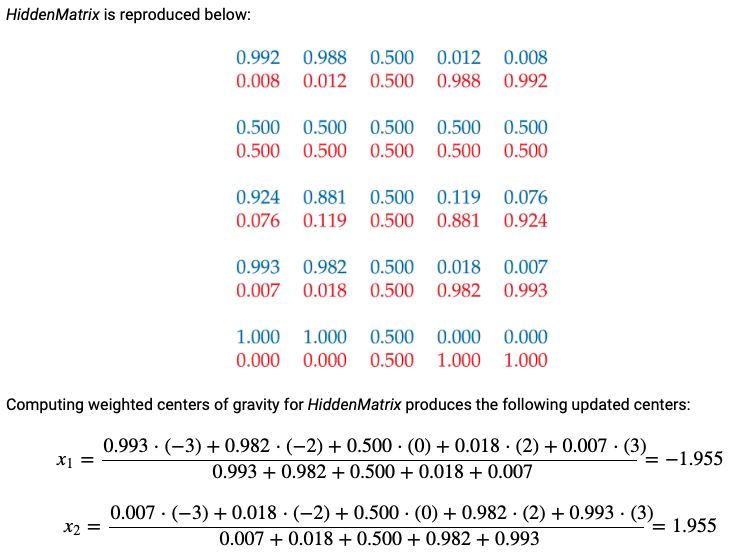
HiddenMatrix的计算方法同上

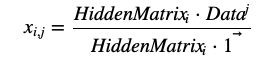
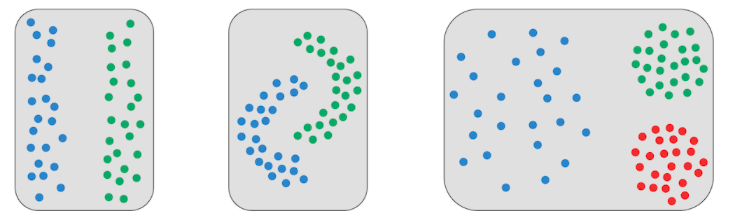
三、Introduction to distance-based clustering

类似于进化树的构建

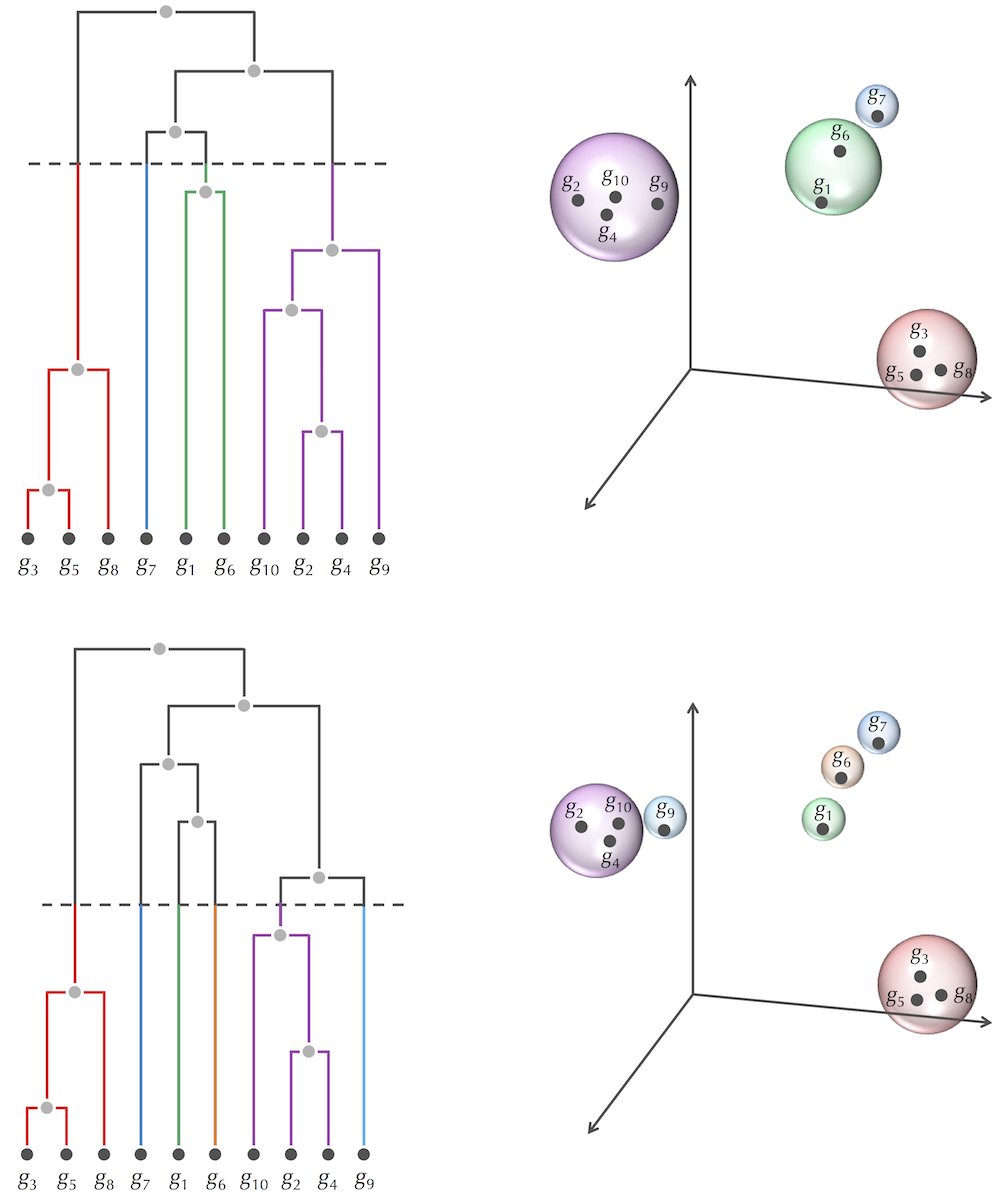
可以完成前两类的聚类，但是第三类不行