Diffusion Model扩散模型
1、扩散模型基本原理:
扩散模型包括两个步骤:
固定的(或预设的)前向扩散过程q:该过程会逐渐将高斯噪声添加到图像中,直到最终得到纯噪声。
2.可训练的反向去噪扩散过程pθ:训练一个神经网络,从纯噪音开始逐渐去噪,直到得到一个真实图像 。
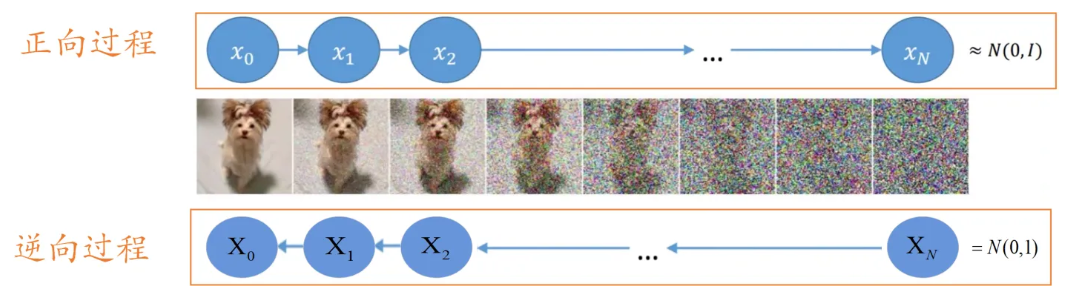
正向过程
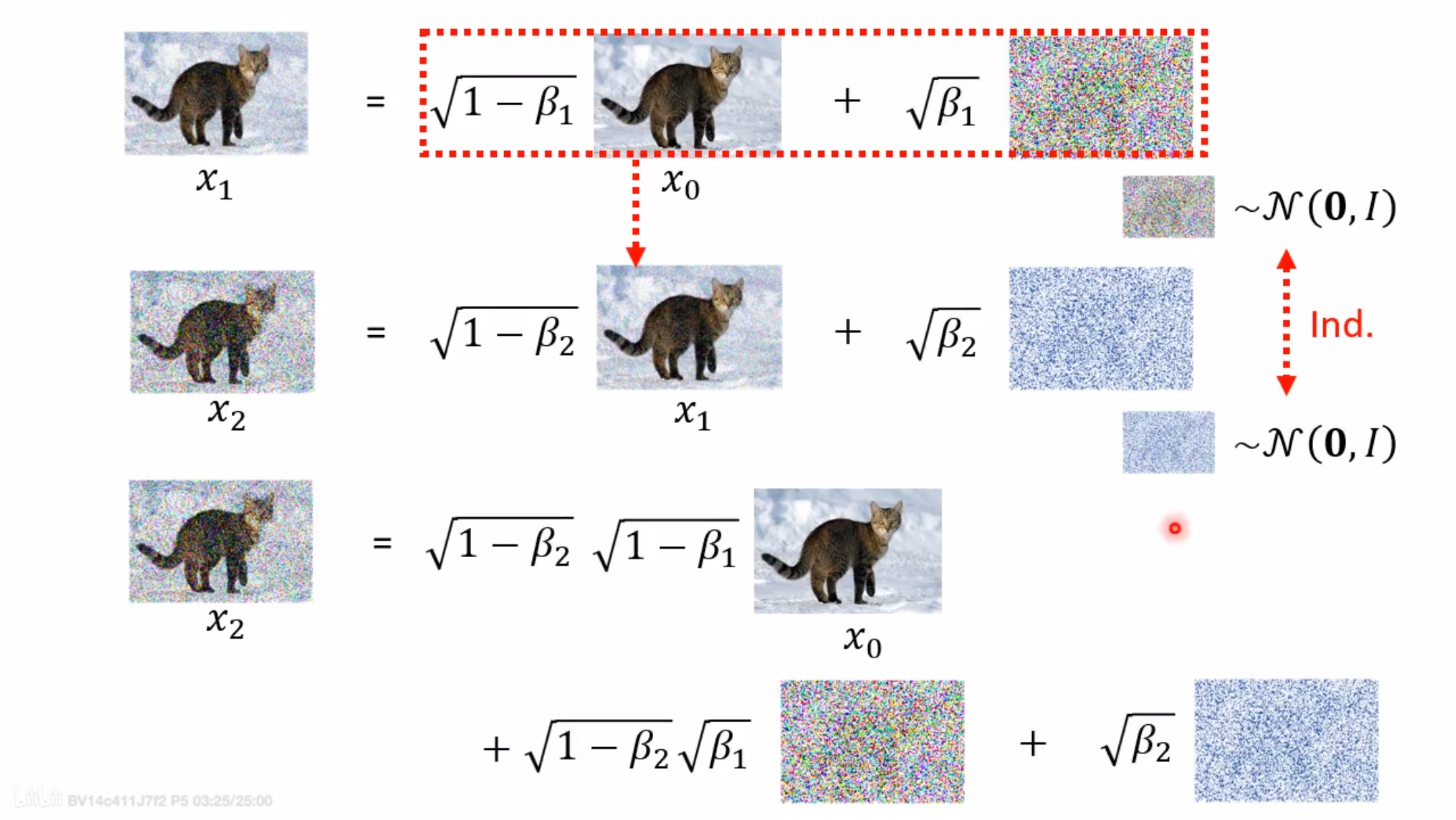
首先,对于一张原始图片,我们给加一个高斯噪声,图片由变成x1。【注意:这里必须要加高斯噪声,因为高斯噪声服从高斯分布,后面的一些运算需要用到高斯分布的一些特性】,重复上述添加高斯噪声步骤,直到图片变成xn,由于添加了足够多的高斯噪声,现在的近似服从高斯分布(又称正态分布)。
每一步添加高斯噪声的量一直是不变的吗? 答案是每步添加高斯噪声的量是变化的,且后一步比前一步添加的高斯噪声更多。我想这一点你通过上图也非常容易理解,一开始原图比较干净,我们添加少量高斯噪声就能对原图产生干扰;但越往后高斯噪声量越多,如果还添加一开始少量的高斯噪声,那么这时对上一步结果基本不会产生任何影响。【注:后文所述的每个时刻图像和这里的每一步图像都是一个意思,如时刻图像表示的就是这个图像】
逆向过程
首先,我们会随机生成一个服从高斯分布的噪声图片,然后一步一步的减少噪声直到生成预期图片。

正向过程实现细节
正向过程其实就是一个不断加噪的过程,后一时刻的图像主要由两个量决定,其一是上一时刻图像,其二是所加噪声量。可以用一个公式来表示时刻和时刻两个图像的关系,如下:

其中,Xt表示t时刻的图像,Xt-1表示t-1时刻图像,Z1表示添加的高斯噪声,其服从N(0,1)分布。【注:N(0,1)表示标准高斯分布,其方差为1,均值为0】
其实,还和另外一个量有关:
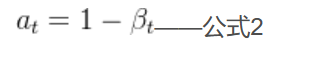
其中,是预先给定的值,它是一个随时刻不断增大的值,论文中它的范围为[0.0001,0.02]。既然
越来越大,则
越来越小,
越来越小,1−
越来越大。

公式4得到了什么——其得到了时刻图像和
时刻图像的关系。按照我们先前的理解,我们再列出
时刻图像和
时刻图像的关系,如下:


很明显的规律,这里我就根据这个规律直接写出 时刻图像和
时刻图像的关系,公式如下:

实际上就是,通过一次次的迭代太慢了,且每一次添加的噪声都独立且满足正态分布,正态分布相加还是正态分布,所以推导出了公式7
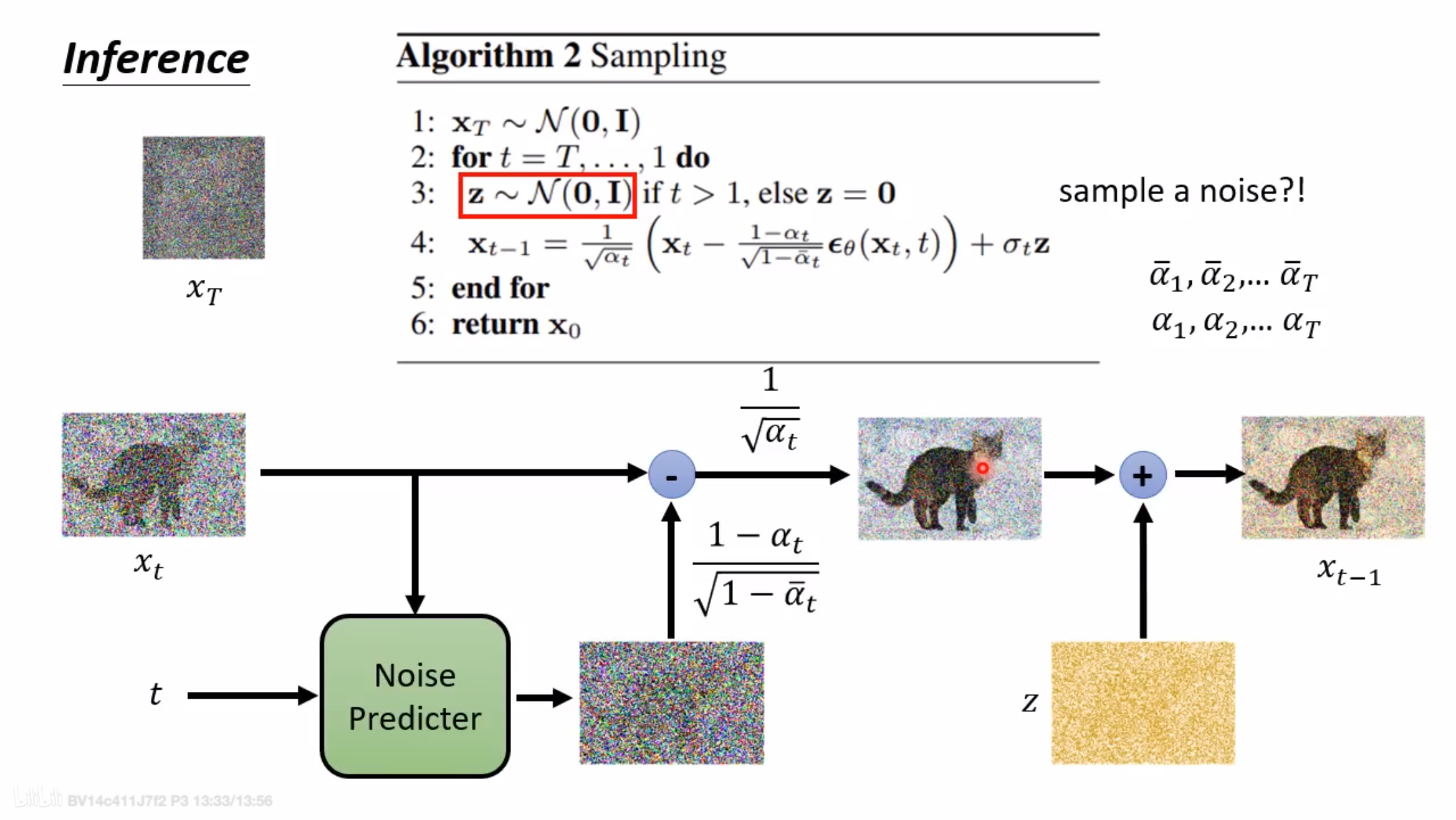
逆向过程实现细节
逆向过程是将高斯噪声还原为预期图片的过程。我们希望将时刻的高斯噪声变成时刻的图像,是很难一步到位的,因此我们思考能不能和正向过程一样,先考虑时刻图像和时刻的关系,然后一步步向前推导得出结论呢。
这里我们需要利用正向过程中的结论,我们在正向过程中可以由时刻图像得到 时刻图像,然后利用贝叶斯公式即可求解。贝叶斯公式的表达式如下:
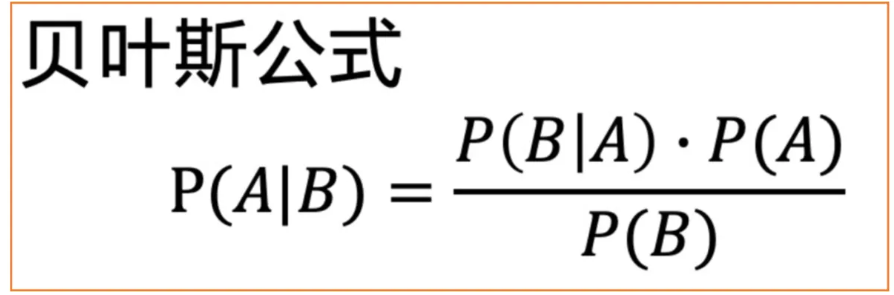
那么我们将利用贝叶斯公式来求时刻图像,公式如下:
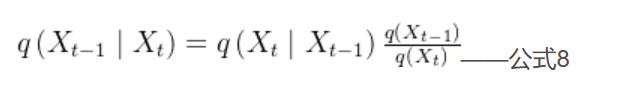
公式8中我们可以求得,就是刚刚正向过程求的嘛。 但
和
是未知的。又由公式7可知,可由
得到每一时刻的图像,那当然可以得到
和
时刻的图像,故将公式8加一个
作为已知条件,将公式8变成公式9,如下:
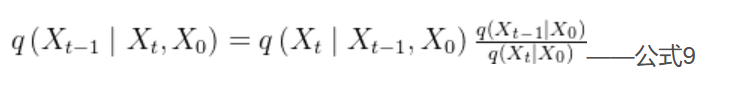
知道了公式9等式右边3项服从的分布,我们就可以计算出等式左边的。这个计算很简单,没有什么技巧,就是纯算。在附录->高斯分布性质部分我们知道了高斯分布的表达式为:
。那么我们只需要求出公式9等式右边3个高斯分布表达式,求出µ和σ,然后进行乘除运算即可求得
。
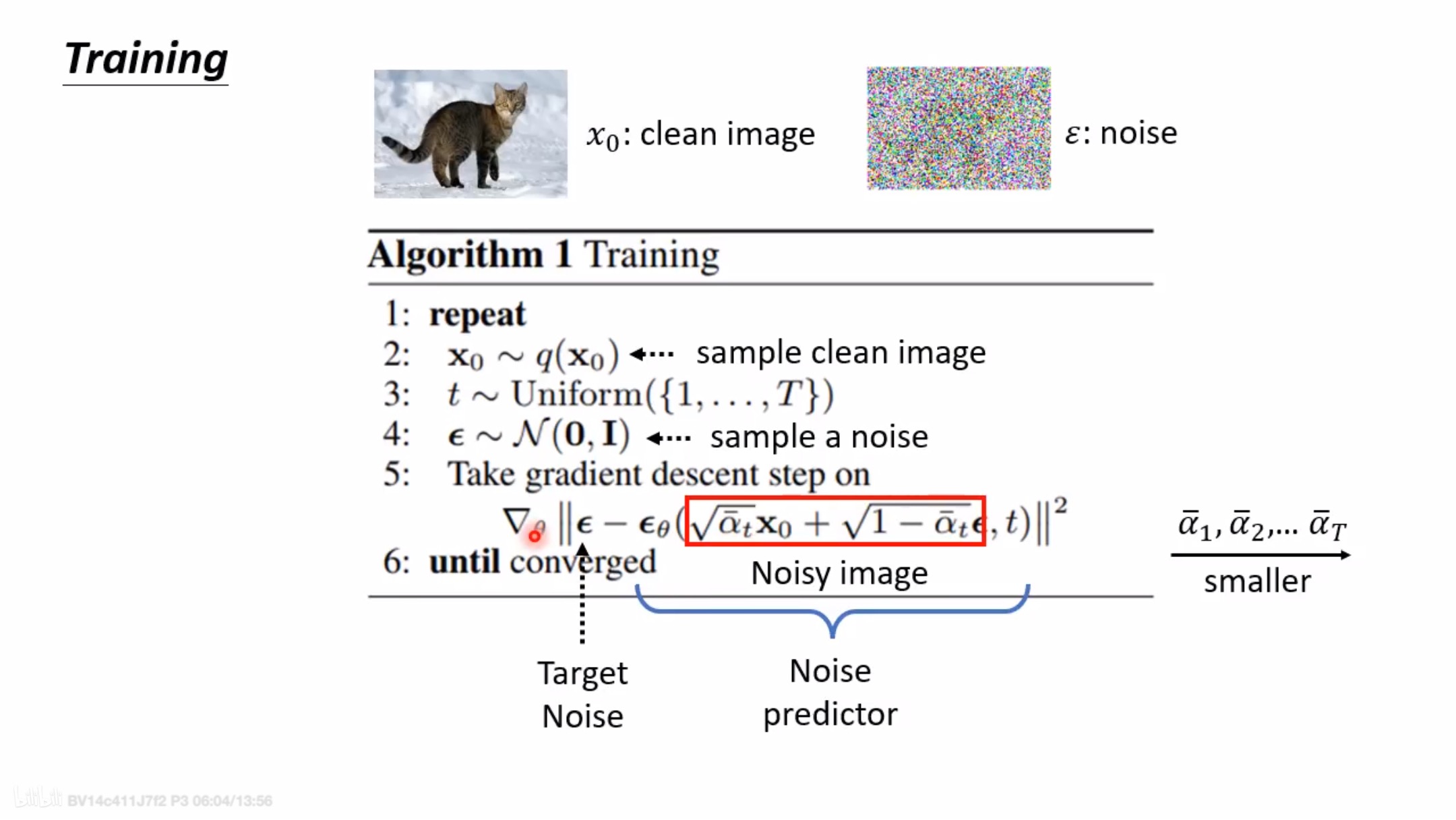
网络训练流程
我们最终要训练的实际上是一个噪声预测器。神经网络输出的噪声是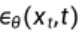 ,而真实的噪声取自于正态分布
,而真实的噪声取自于正态分布 ,则损失函数为:
,则损失函数为:
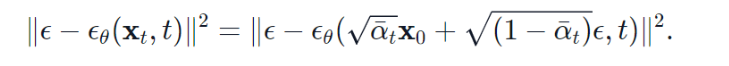
高斯分布性质
高斯分布又称正态分布,其表达式为:
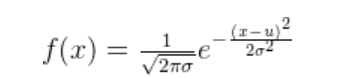
其中为均值,
为方差。若随机变量服
从正态均值为
,方差为
的高斯分布,一般记为
。此外,有一点大家需要知道,如果我们知道一个随机变量服从高斯分布,且知道他们的均值和方差,那么我们就能写出该随机变量的表达式。
高斯分布还有一些非常好的性质:
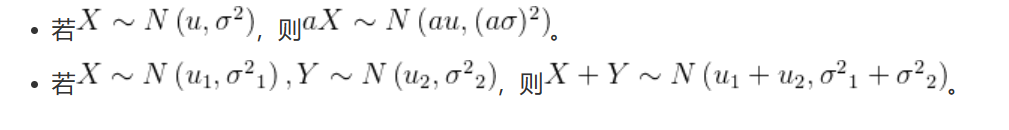
Diffusion Model扩散模型的更多相关文章
- 一文详解扩散模型:DDPM
作者:京东零售 刘岩 扩散模型讲解 前沿 人工智能生成内容(AI Generated Content,AIGC)近年来成为了非常前沿的一个研究方向,生成模型目前有四个流派,分别是生成对抗网络(Gene ...
- A Neural Influence Diffusion Model for Social Recommendation 笔记
目录 一.摘言 二.杂记 三.问题定义和一些准备工作 四.模型真思想 五.实验部分 六.参考文献 一.摘言 之前协同过滤利用user-item交互历史很好的表示了user和item.但是由于用户行为的 ...
- Hugging Face 每周速递: 扩散模型课程完成中文翻译,有个据说可以教 ChatGPT 看图的模型开源了
每一周,我们的同事都会向社区的成员们发布一些关于 Hugging Face 相关的更新,包括我们的产品和平台更新.社区活动.学习资源和内容更新.开源库和模型更新等,我们将其称之为「Hugging Ne ...
- Model Validation(模型验证)
Model Validation(模型验证) 前言 阅读本文之前,您也可以到Asp.Net Web API 2 系列导航进行查看 http://www.cnblogs.com/aehyok/p/344 ...
- 008.Adding a model to an ASP.NET Core MVC app --【在 asp.net core mvc 中添加一个model (模型)】
Adding a model to an ASP.NET Core MVC app在 asp.net core mvc 中添加一个model (模型)2017-3-30 8 分钟阅读时长 本文内容1. ...
- Box Model 盒子模型
Box Model盒子模型,是初学者在学习HTMl5时会学到的一个重要的模型,也有一些人称它为框模型,因为盒子是属于3维,而框是平面的.称之为盒子模型,是因为其结构和盒子十分相似,其最外面是margi ...
- Consistency Models终结扩散模型
最近看到一篇论文,觉得特别有意思,并且在学术界引起了不小的动静,他就是一致性模型,据说图像生成效果快.质量高,并且还可以实现零样本图像编辑,即不进行一些视觉任务训练,可以实现图像超分.修复.上色等功能 ...
- Maximum Entropy Model(最大熵模型)初理解
0,熵的描述 熵(entropy)指的是体系的混沌的程度(可也理解为一个随机变量的不确定性),它在控制论.概率论.数论.天体物理.生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义, ...
- CSS Box Model 盒子模型
1. 介绍 1.1 什么是 Box Model 在HTML中的每个element(元素)都可以看作一个矩形的盒子,矩形从内到外依次由元素的内容(content).内边距(padding).边框(bor ...
- Keras Model Sequential模型接口
Sequential 模型 API 在阅读这片文档前,请先阅读 Keras Sequential 模型指引. Sequential 模型方法 compile compile(optimizer, lo ...
随机推荐
- iOS视图控件的内容显示和离屏渲染流程
iOS中UI控件内容显示流程 UIKit界面组成 iOS中组成页面的各个元素基本来自UIKit,我们可以修改布局或自定义绘制来修改UIKit元素的默认展示. UIView的页面显示内容有CALayer ...
- 【python技巧】替换文件中的某几行
[python技巧]替换文件中的某几行 1. 背景描述 最近在写一个后端项目,主要的操作就是根据用户的前端数据,在后端打开项目中的代码文件,修改对应位置的参数,因为在目前的后端项目中经常使用这个操作, ...
- 使用antd-mobile遇到的坑
在使用antd-mobile中的组件的时候,遇到了一些比较棘手的问题,经过查找相关资料和网上的帮助,在此整理出了问题以及解决办法: 在引入antd-mobile的时候,根据官网提供的文档: 1,首先安 ...
- 使用GPU搭建支持玛雅(Maya)和Adobe AI,DW,PS的职校云计算机房
背景 学校为职业学校,计算机教室需要进行Maya.Adobe Illustrator.Adobe Dreamweaver.Adobe PhotoShop等软件的教学.每个教室为35用户.资源需求为4核 ...
- CFS-GA 相关性特征选择与遗传算法 特征选择/特征提取
CFS-GA特征选择/特征提取 CFS 对于一个样本空间,构造一个二维矩阵A代表此样本空间,A中每行代表一条数据,每列代表一个特征 样本中的数据分为数个特征,其中\(A_i\)表示第\(i\)个特征, ...
- DDMS查看Threads情况
有时候程序运行出现死锁或者信号量卡死是很纠结的问题,单看代码很难分析定位问题,这时候可以借助DDMS来查看threads的运行情况,一目了然. 手机连接上USB,确保adb连通,然后启动Eclipse ...
- 高可用mongodb集群(分片+副本):用户权限配置
目录 ■ 创建副本集认证的key文件 ■ 修改配置文件指定keyfile ■ 重新启动节点 ■ 创建帐号和认证 ■ 用管理员帐号可查看整体的分片情况 ■ 用普通帐号访问数据 ■ 客户端连接多个mong ...
- SQL 语句 增删改查、边学习边增加中..... 这一部分为select
SQL语句按照最大的类别分为 1.增加 insert 2.删除 delete https://www.cnblogs.com/kuangmeng/p/17756654.html 3.修改update ...
- 循序渐进介绍基于CommunityToolkit.Mvvm 和HandyControl的WPF应用端开发(8) -- 使用Converter类实现内容的转义处理
在我们WPF应用端的时候,和WInform开发或者Vue前端开发一样,有时候也需要对内容进行转义处理,如把一些0,1数值转换为具体含义的文本信息,或者把一些布尔变量转换为是否等,都是常见的转换处理,本 ...
- seed 随机种子的作用
在随机数生成中,种子(seed)是一个起始值,用于确定随机数生成器的初始状态.通过设置相同的种子,可以确保每次运行程序时生成的随机数序列都是相同的.这种确定性的随机数生成可以带来以下几个好处: 可复现 ...
