Atm/抢掠计划——题解

题目描述

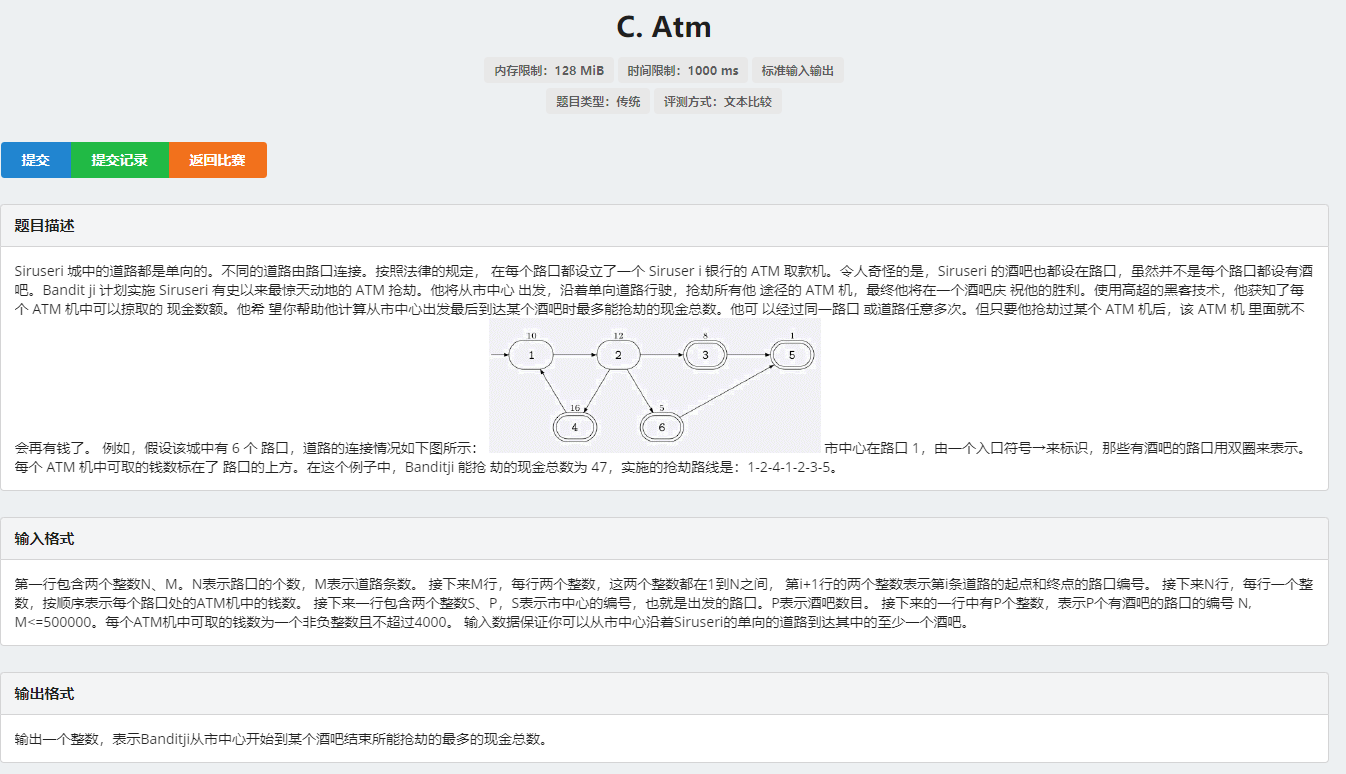
样例

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1 5
1 4
4
3
5
6

47

解析

题目明显是最长路，可以用spfa求最长路，但数据范围5e5明显不允许，所以我们可以用tarjan优化一下，然后这就变成了一道

tarjan板子题，先用tarjan缩点，点权为几个点之和，把所有点再存到一个数组中，再按之前建图关系，把不在一个块的点连边

再跑一遍spfa就可以了

solution

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+5;
const int INF=0x7f7f7f7f;
int tot,head[MAXN],nxt[MAXN<<1],to[MAXN<<1],pre[MAXN],vis[MAXN],low[MAXN];
int n,m,s,st,t,h,r,c,d,cnt,now,ans,w,sum,num,val[MAXN],id[MAXN],out[MAXN];
int a[MAXN],b[MAXN],bill[MAXN],x[MAXN],y[MAXN],dis[MAXN];
void add(int x,int y)
{
    to[++tot]=y;
    nxt[tot]=head[x];
    head[x]=tot;
}
stack<int>p;
void tarjan(int u)
{
    pre[u]=low[u]=++cnt;
    p.push(u);
    vis[u]=1;
    for(int i=head[u];i;i=nxt[i])
    {
        int y=to[i];
        if(!pre[y])
        {
            tarjan(y);
            low[u]=min(low[u],low[y]);
        }
        else if(vis[y])
        {
            low[u]=min(low[u],pre[y]);
        }
    }
    if(low[u]==pre[u])
    {
        num++;
        int temp=-1;
        while(temp!=u){
            temp=p.top();
            p.pop();
            vis[temp]=0;
            id[temp]=num;//把所有点再存到这个数组中
            val[num]+=a[temp];//块点权为所有包含点之和
            if(b[temp]) bill[num]=1;//如果缩进的点有酒吧，则本块又酒吧
        }
    }
}
queue<int>q;
void spfa()//spfa求最长路
{
	memset(dis,-0x7f7f7f7f,sizeof(dis));
	q.push(id[st]);
    dis[id[st]]=val[id[st]];//先加上本点点权，以后跑的边的边权即为边通向点的点权
	//vis[st]=true;
	while(!q.empty())
	{
		s=q.front();
		q.pop();
		vis[s]=false;
		for(int i=head[s];i;i=nxt[i])
		{
			int y=to[i];
			if(dis[y]<dis[s]+val[y])//保证权值为正，不用判负环
			{
				dis[y]=dis[s]+val[y];
				if(!vis[y])
				{
					q.push(y);
					vis[y]=true;
				}
			}
		}
	}
    ans=-INF;
    for(int i=1;i<=num;i++)
    {
        if(bill[i]) ans=max(ans,dis[i]);//只看有酒吧的
    }
    printf("%d",ans);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&r,&c);
        x[i]=r,y[i]=c;//记录链接点
        add(r,c);
    }
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    scanf("%d%d",&st,&t);
    for(int i=1;i<=t;i++)
    {
        scanf("%d",&d);
        b[d]=1;//有酒吧
    }
    for(int i=1;i<=n;i++)if(!pre[i]) tarjan(i);
    memset(head,0,sizeof(head));//缩点后重建图，初始化
    tot=0;
    for(int i=1;i<=m;i++) if(id[x[i]]!=id[y[i]]) add(id[x[i]],id[y[i]]);//原本连通的点是否在同一个块中，不在的建边
    spfa();
    return 0;
}