Python汉诺塔问题递归算法与程序

汉诺塔问题：

问题来源：汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从上往下从小到大顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘，只能移动在最顶端的圆盘。有预言说，这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩，当然这个传说并不可信，如今汉诺塔更多的是作为一个玩具存在。

现在有n个圆盘从上往下从小到大叠在第一根柱子上，要把这些圆盘全部移动到第三根柱子要怎么移动呢？请找出需要步骤数最少的方案

因此我们可以将问题简化描述为：n个盘子和3根柱子：A(源)、B(备用)、C(目的)，盘子的大小不同且中间有一孔，可以将盘子“串”在柱子上，每个盘子只能放在比它大的盘子上面。起初，所有盘子在A柱上，问题是将盘子一个一个地从A柱子移动到C柱子。移动过程中，可以使用B柱，但盘子也只能放在比它大的盘子上面。

因此我们得出汉诺塔问题的以下几个限制条件：

1.在小圆盘上不能放大圆盘。 

2.在三根柱子之间一回只能移动一个圆盘。 

3.只能移动在最顶端的圆盘。 

首先，我们从简单的例子开始分析，然后再总结出一般规律。

当n = 1的时候，即此时只有一个盘子，那么直接将其移动至C即可。移动过程就是 A -> C

当n = 2的时候，这时候有两个盘子，那么在一开始移动的时候，我们需要借助B柱作为过渡的柱子，即将A柱最上面的那个小圆盘移至B柱，然后将A柱底下的圆盘移至C柱，最后将B柱的圆盘移至C柱即可。那么完整移动过程就是A -> B , A -> C , B -> C

当n = 3的时候，那么此时从上到下依次摆放着从小到大的三个圆盘，根据题目的限制条件：在小圆盘上不能放大圆盘，而且把圆盘从A柱移至C柱后，C柱圆盘的摆放情况和刚开始A柱的是一模一样的。所以呢，我们每次移至C柱的圆盘（移至C柱后不再移到其他柱子上去），必须是从大到小的，即一开始的时候，我们应该想办法把最大的圆盘移至C柱，然后再想办法将第二大的圆盘移至C柱......然后重复这样的过程，直到所有的圆盘都按照原来A柱摆放的样子移动到了C柱。

那么根据这样的思路，问题就来了：  如何才能够将最大的盘子移至C柱呢？  那么我们从问题入手，要将最大的盘子移至C柱，那么必然要先搬掉A柱上面的n-1个盘子，而C柱一开始的时候是作为目标柱的，所以我们可以用B柱作为"暂存"这n-1个盘子的过渡柱，当把这n-1的盘子移至B柱后，我们就可以把A柱最底下的盘子移至C柱了。 

而接下来的问题是什么呢？  我们来看看现在各个柱子上盘子的情况，A柱上无盘子，而B柱从上到下依次摆放着从小到大的n-1个盘子，C柱上摆放着最大的那个盘子。 所以接下来的问题就显而易见了，那就是要把B柱这剩下的n-1个盘子移至C柱，而B柱作为过渡柱，那么我们需要借助A柱，将A柱作为新的"过渡"柱，将这n-1个盘子移至C柱。 

根据上面的分析，我们可以抽象得出这样的结论：

汉诺塔函数原型：

我们把n个盘子从A柱移动至C柱的问题可以表示为： Hanio(n,A,B,C);  那么从上面的分析得出：  该问题可以分解成以下子问题： 

第一步：将n-1个盘子从A柱移动至B柱（借助C柱为过渡柱） 

第二步：将A柱底下最大的盘子移动至C柱 

第三步：将B柱的n-1个盘子移至C柱（借助A柱为过渡柱） 

…….

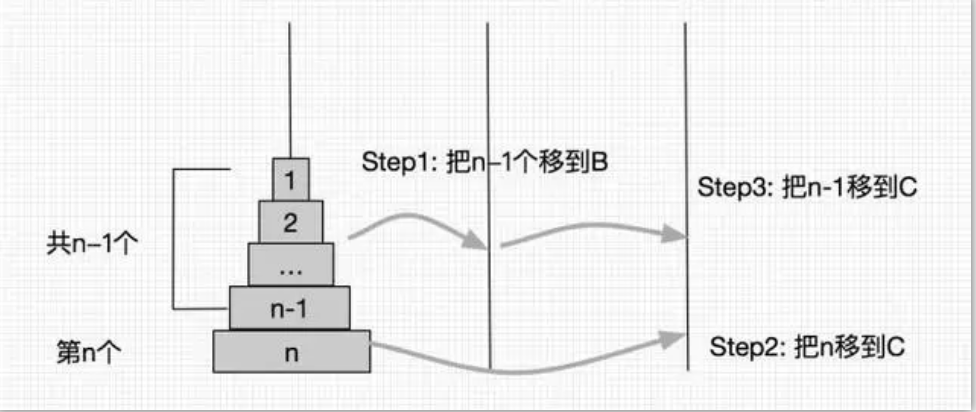
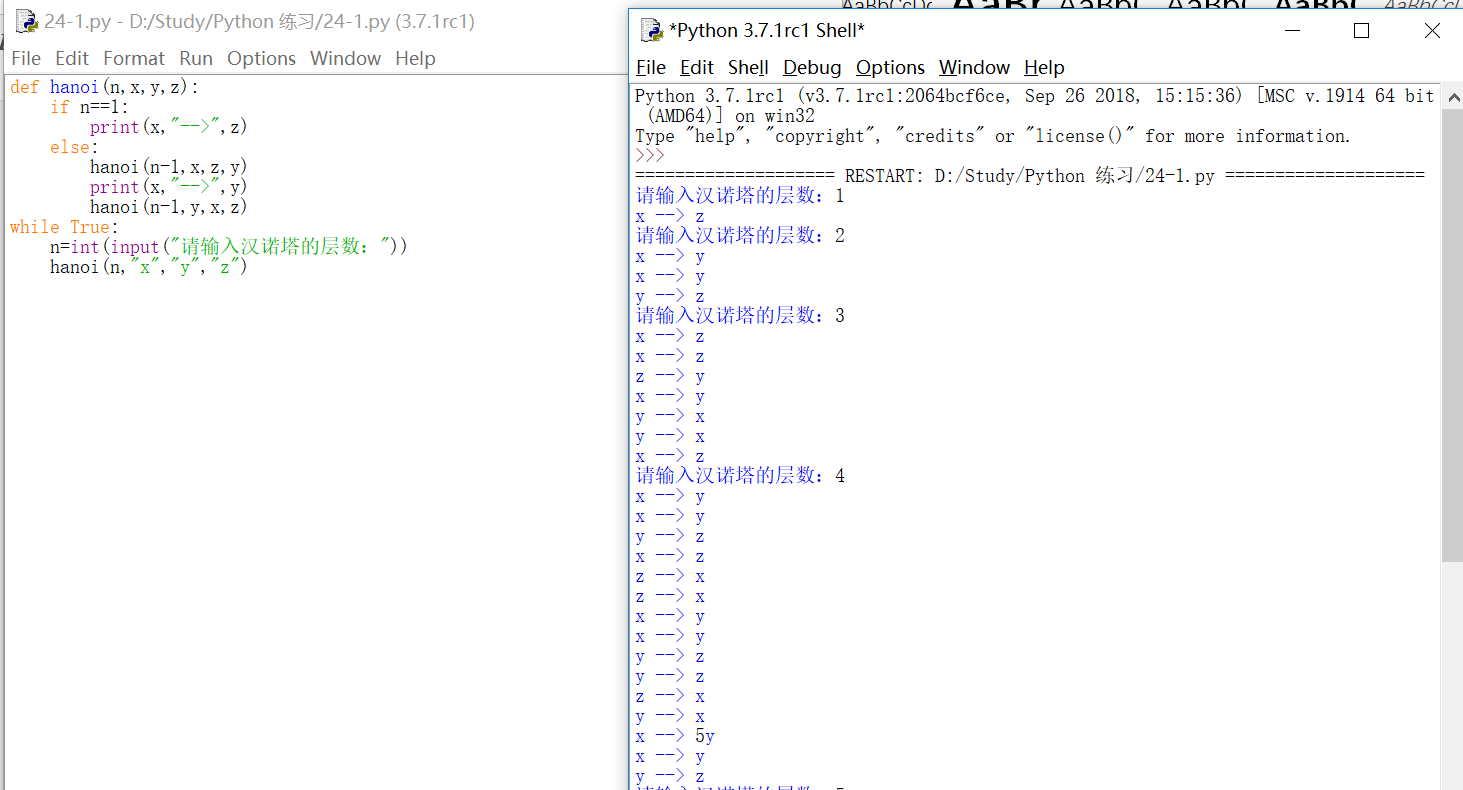
因此利用python编程规则其完整代码如下所示：

def hanoi(n,x,y,z):

    if n==1:

       
print(x,"-->",z)

    else:

        hanoi(n-1,x,z,y)

       
print(x,"-->",y)

        hanoi(n-1,y,x,z)

while True:

    n=int(input("请输入汉诺塔的层数："))

   
hanoi(n,"x","y","z")