网页排名算法PagaRank

网页排名算法PageRank

PageRank，网页排名，又叫做网页级别。是一种利用网页之间的超链接数据进行计算的方法。它是由Google的两位创始人提出的。

对于用户而言，网页排名一般是比较主观的，但也存在一些方法可以给出较为客观的排名，PageRank就是其中一种。它衡量的是网页之间的相对重要性，把每一个网页当成一个图结点，网页之间的超链接当成是结点之间的边，根据结点之间的链接关系来进行计算的，核心思想是一个网页被链接的次数越多，那么它就越受关注。

1.简单PR模型

假设有这样几个网页的图，他们的连接关系如下：



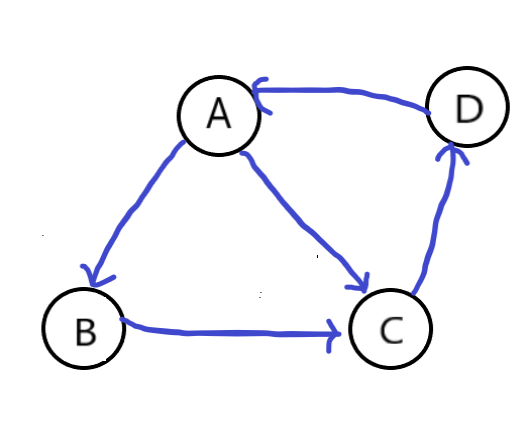
我们这样来看，这里有四个网页，分别是A，B，C，D，他们之间的连接用边表示。所以，A有两个外链接，出度为2，分别指向B和C，B有一个外链接，指向C。反过来，C就有两个入链，也就是入度为2。

因此，一个网页的影响力 = 所有入链集合的中页面的影响力的加权和，计算公式为：

\[PR(u) = \sum_{v\in IN_{u}} \frac{PR(v)}{N(v)}
\]

其中，u是当前要计算影响力的页面，\(IN_{u}\)是u的入链集合，\(N(v)\)是页面v的出链总数。把它当成是一个投票的过程，规定每个页面可以且仅可以投一票，它投的票的影响力大小就是它自身的影响力大小，由于只能投一票，所以它如果投给了多个网页，那么被投的网页只能把它的票撕开，平分。然后，大家互相投票，每投完一轮票之后，统计大家的得到的票数，就能够得到每个网页的新的影响力大小。

实际上，每个网页投给给其他网页的票数相当于一个跳转概率，以A为例，它投票给了B和C，所以用户在访问A时，跳转到B和C的概率都为1/2。

我们把每个网页对其他网页的投票写成一个列向量的形式，如对A

\[M_{A}=\begin{bmatrix}0\\1/2\\1/2\\0\\ \end{bmatrix}
\]

四个列向量组合起来，就变成了一个转移矩阵：

\[M=\begin{bmatrix}0 & 0 & 0 & 1\\ 1/2 & 0 & 0 & 0\\ 1/2 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix}
\]

有了这个转移矩阵，我们在给定一个初始的影响力向量，就可以通过迭代的方式，不断计算计算新的影响力，直到收敛为止。

初始化每个页面的影响力都相同，为

\[W_{0} =\begin{bmatrix}1/4\\1/4\\1/4\\1/4\\ \end{bmatrix}
\]

一次计算后得到：

\[W_{1} =\begin{bmatrix}0 & 0 & 0 & 1\\ 1/2 & 0 & 0 & 0\\ 1/2 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix}\begin{bmatrix}1/4\\1/4\\1/4\\1/4\\ \end{bmatrix}=\begin{bmatrix}0.25\\0.125\\0.375\\0.25 \end{bmatrix}
\]

经过n（有限）次迭代后：

\[W_{n} =\begin{bmatrix}0 & 0 & 0 & 1\\ 1/2 & 0 & 0 & 0\\ 1/2 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{bmatrix}^n
\begin{bmatrix}1/4\\1/4\\1/4\\1/4\\ \end{bmatrix}
=\begin{bmatrix}0.28613281\\0.14367676\\0.28588867\\0.28430176 \end{bmatrix}\]

这个最终求出来的收敛的值就是我们想要得到的网页的理论影响力大小，把它按照从大到小的顺序排列起来，就是网页的排名了。比如这里的排名是A>C>D>B。

代码实现（基于Python）

import numpy as np

#简易版
def pageRank1(G,delta):
    #G为一个方阵，描述了结点间的游走概率
    #delta为可接受误差，只要迭代过程中，前后两次算出来的权重列向量的差方小于delta，就认为收敛了
    n = G.shape[0]  #n为矩阵行数（结点个数）
    w = np.ones(n)*(1/n)   #初始化每个页面的权重，w是一个长为n的列向量，每个元素代表该网页的权重，初始值为1/n
    maxIter = 1000   #最大迭代次数为1000次
    for i in range(0,maxIter):
        tw = w       #暂存上次记录
        w = np.dot(G,w)     #计算新的概率
        err = np.power((tw-w),2)  #做差取平方
        if(sum(err)<delta): #若收敛了，就停止迭代
            break
    return w          #返回计算的结果

2.修正的PR模型

实际上，上面讨论的只是最基本的模型思想。这个简单的模型还是存在着不少缺陷，比如说，如果某个网页没有链接到其他网页的出链，那么，它的转移列向量就全是0了，也就是对应的转移矩阵里存在一个全为0的列。这样的话，在迭代的过程中，那个网页就像一个黑洞一样，渐渐的吸收其他网页的权重，但是不输出，最终导致全部权重都变成了0。显然这样是不行的，所以一个解决的方法是，对任何一个页面，用户都有一定的概率直接（输入链接地址）去访问，这样，就可以避免这种情况的发生。

于是，引入一个新的量d，叫做阻尼系数，描述的是用户不会随机跳转到某一网页的概率，那1-d就是他会随机跳转到该页面的概率，所以上面的公式修改为：

\[PR(u) = (1-d) + d\sum_{v\in IN_{u}} \frac{PR(v)}{N(v)}
\]

下面给出修正版的实现，也很简单

#修正版
def pageRank2(G,D,E=0.00001):
    #D是阻尼系数
    #E是可接受误差
    n = G.shape[0]  #n为矩阵行数（结点个数）
    w = np.ones(n)*(1/n)
    maxIter = 1000   #最大迭代次数为1000次
    for i in range(0,maxIter):
        tw = w       #暂存上次记录
        w = (1-D)/ n + D * np.dot(G, w)     #计算新的概率
        err = np.power((tw - w), 2)  #做差取平方
        if(sum(err)<E):
            break
    return w

3.简单总结

以上就是对pr算法的简单理解与实现，其实核心思想很简单，就是一个网页它拥有的“粉丝”越多或者它的“粉丝”本身就很具备影响力的话，那就可以推断它的影响力相应的也比较大，对应到计算层面就是用了转移矩阵和初始影响力向量做多次乘积运算，直到找到一个接近稳定的值作为网页的影响力。

参考资料：

【1】机器学习经典算法之PageRank https://www.cnblogs.com/jpcflyer/p/11180263.html

【2】PageRank算法原理与实现 https://blog.csdn.net/leadai/article/details/81230557