BZOJ4036 按位或

解：有两种做法......

第一种，按照秘密袭击coat的套路，我们只需要求出即可。因为一种操作了i次的方案会被恰好计数i次。

那么这个东西怎么求呢？直接用FWT的思想，对于一个状态s，求出选择s所有子集的概率p_s。那么第i次操作后是s的子集的概率就是p_sⁱ。

设f_s表示第i次操作之后是s的子集的概率。

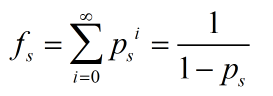
把所有的f求出来之后做一次IFWT即可。然后我们对于所有非全集求和。

参考资料。

 #include <bits/stdc++.h>

 const int N = , M = ;
 const double eps = 1e-;

 double f[M], p[M], w[M];
 int cnt[M], pw[M], n, lm;

 inline void FWT_or(double *a, int n, int f) {
     for(int len = ; len < n; len <<= ) {
         for(int i = ; i < n; i += (len << )) {
             for(int j = ; j < len; j++) {
                 a[i + len + j] += f * a[i + j];
             }
         }
     }
     return;
 }

 int main() {
     scanf("%d", &n);
     lm =  << n;
     for(int i = ; i < lm; i++) {
         scanf("%lf", &p[i]);
         w[i] = p[i];
         if(i) {
             cnt[i] =  + cnt[i - (i & (-i))];
         }
         if(i > ) {
             pw[i] = pw[i >> ] + ;
         }
     }
     FWT_or(p, lm, );
     for(int i = ; i < lm; i++) {
         if(i != lm -  && p[i] >  - eps) {
             puts("INF");
             return ;
         }
         f[i] = 1.0 / ( - p[i]);
     }
     FWT_or(f, lm, -);
     double ans = ;
     for(int i = ; i < lm - ; i++) {
         ans += f[i];
     }
     printf("%.10f\n", ans);
     return ;
 }

AC代码

第二种：Min-Max容斥。

设f_s为把状态s的所有元素中至少一个变成1的期望次数。

同样是对步数0~∞求和，每次的概率是(没选到)ⁱ。最后Min-Max容斥统计答案。

 #include <bits/stdc++.h>

 const int N = , M = ;
 const double eps = 1e-;

 double f[M], p[M], w[M];
 int cnt[M], pw[M], n, lm;

 inline void FWT_or(double *a, int n, int f) {
     for(int len = ; len < n; len <<= ) {
         for(int i = ; i < n; i += (len << )) {
             for(int j = ; j < len; j++) {
                 a[i + len + j] += f * a[i + j];
             }
         }
     }
     return;
 }
 /*
 2
 0.25 0.25 0.25 0.25

 */
 int main() {
     scanf("%d", &n);
     lm =  << n;
     for(int i = ; i < lm; i++) {
         scanf("%lf", &p[i]);
         w[i] = p[i];
         if(i) {
             cnt[i] =  + cnt[i - (i & (-i))];
         }
         if(i > ) {
             pw[i] = pw[i >> ] + ;
         }
     }
     FWT_or(p, lm, );
     for(int i = ; i < lm; i++) {
         if(i != lm -  && p[i] >  - eps) {
             printf("INF\n");
             return ;
         }
         //printf("p %d = %lf \n", i, p[i]);
         f[i] = 1.0 / ( - p[(lm - ) ^ i]);
     }
     //FWT_or(f, lm, -1);
     double ans = ;
     for(int i = ; i < lm; i++) {
         if(cnt[i] & ) ans += f[i];
         else ans -= f[i];
     }
     printf("%.10f\n", ans);
     return ;
 }

AC代码