洛谷P2846 光开关Light Switching

题目描述

灯是由高科技——外星人鼠标操控的。你只要左击两个灯所连的鼠标，

这两个灯，以及之间的灯都会由暗变亮，或由亮变暗。右击两个灯所连的鼠

标，你就可以知道这两个灯，以及之间的灯有多少灯是亮的。起初所有灯都是暗的，你的任务是在\(LZ\)之前算出灯的亮灭。

输入输出格式

输入格式：

第1 行: 用空格隔开的两个整数\(N\) 和\(M\)，\(N\) 是灯数

第\(2..M+1\) 行: 每行表示一个操作, 有三个用空格分开的整数: 指令号, \(S_i\) 和\(E_i\)

第\(1\) 种指令(用\(0\) 表示)包含两个数字\(S_i\) 和\(E_i\) (\(1 \leq S_i \leq E_i \leq N\)), 它们表示起

始开关和终止开关. 表示左击

第\(2\) 种指令(用\(1\) 表示)同样包含两个数字\(S_i\) 和\(E_i\) (\(1 \leq S_i \leq E_i \leq N\)), 不过这

种指令是询问从\(S_i\) 到\(E_i\) 之间的灯有多少是亮着的.

输出格式：

输入输出样例

输入样例#1：

4 5
0 1 2
0 2 4
1 2 3
0 2 4
1 1 4

输出样例#1：

1
2

说明

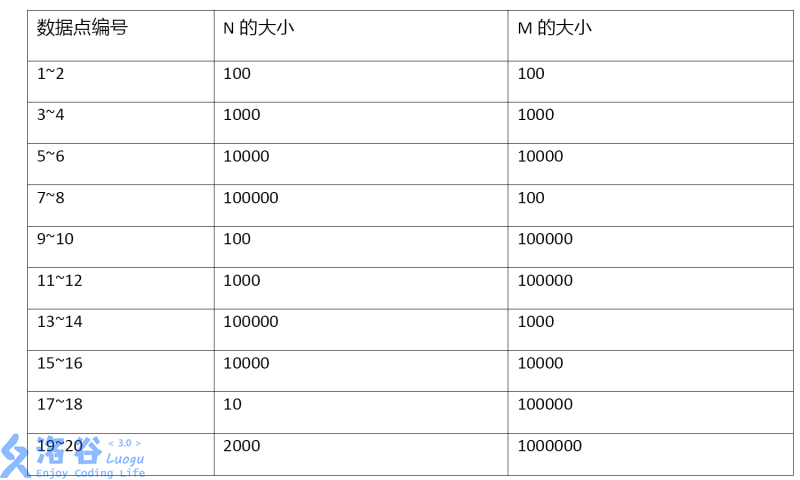
思路：这道题目涉及到区间修改和区间查询，因此可以用线段树来维护，那该怎么维护呢？继续观察，可以发现，因为刚开始所以灯都是关着的，然后修改一次就灯的状态就会变化一次，我们可以用\(1\)和\(0\)分别代替开关状态，那么修改操作不就成了区间异或运算么？查询操作不就成了查询区间中\(1\)的个数了么？而且初始值都是0，所以无需建树，然后用线段树维护一个区间\(1\)的个数即可。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int n,m,sum[maxn<<2],lazy[maxn<<2];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void pushup(int rt) {
  sum[rt]=sum[ls]+sum[rs];
}
inline void pushdown(int rt, int len) {
  if(lazy[rt]) {
    lazy[ls]^=1;
    lazy[rs]^=1;
    sum[ls]=(len-(len>>1))-sum[ls];
    sum[rs]=(len>>1)-sum[rs];
    lazy[rt]=0;
  }
}
void modify(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return;
  if(L<=l&&r<=R) {
    sum[rt]=r-l+1-sum[rt];
    lazy[rt]^=1;
    return;
  }
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  modify(ls,l,mid,L,R),modify(rs,mid+1,r,L,R);
  pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return 0;
  if(L<=l&&r<=R) return sum[rt];
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
int main() {
  n=qread(),m=qread();
  for(int i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(!k) modify(1,1,n,l,r);
    else printf("%d\n",csum(1,1,n,l,r));
  }
  return 0;
}