小小c#算法题 - 11 - 二叉树的构造及先序遍历、中序遍历、后序遍历

在上一篇文章 小小c#算法题 - 10 - 求树的深度中，用到了树的数据结构，树型结构是一类重要的非线性数据结构，树是以分支关系定义的层次结构，是n（n>=0)个结点的有限集。但在那篇文章中，只是简单地把结点组合到了一块。

这次，我们来简单定义一棵二叉树的数据结构，并实现其先序（根）遍历、中序（根）遍历、后序（根）遍历算法。

下面先来看一下先序遍历，中序遍历，后序遍历的定义：

先序遍历：

若二叉树为空，则空操作，否则

（1）访问根结点；

（2）先序遍历左子树；

（3）先序遍历右子树；

中序遍历：

若二叉树为空，则空操作，否则

（1）中序遍历左子树；

（2）访问根结点；

（3）中序遍历右子树；

后序遍历：

若二叉树为空，则空操作，否则

（1）后序遍历左子树；

（2）后序遍历右子树；

（3）访问根结点；

从上面定义可以看出，三种遍历算法都是一个递归的过程，临界条件为根结点为null，即要遍历的树为空树。

树既然是结点的数据结构，那么就先来定义结点的数据结构，下面是二叉树的结点结构：

    public class Node
    {
        public int value;
        public Node leftChild;
        public Node rightChild;
        public void Display()
        {
            Console.Write(value + "  ");
        }
    }

通过代码可以看到，一个结点由以下元素组成：值(value)；左孩子的引用(leftChild)；右孩子的引用(rightChild)；显示方法(Display)，这个方法用于测试与验证工作，用来输出结点的值到终端。其中值(value)属性的定义可以为任何复杂类型的结构，这里只是为了方便，定义为了一个整型变量。

下面就来定义二叉树了，其实树可以有很多属性或方法，比如，可以有插入一个结点作为一个结点结点的左孩子，右孩子的方法，求一个结点的兄弟结点的方法，求树深度的方法，求一个结点父结点的方法等等。在这篇文章中，我们只给出1个属性和5个方法。树的根结点属性，构造函数，插入结点方法，先序遍历方法，中序遍历方法，后序遍历方法。

先给出树的完整代码：

    public class BinaryTree
    {
        public Node root;

        public BinaryTree()
        {
            root = null;
        }

        public void Insert(int data)
        {
            Node newNode = new Node() { value = data };
            if (root == null)
            {
                root = newNode;
            }
            else
            {
                Node current = root;
                Node parent;
                while (true)
                {
                    parent = current;
                    if (data < current.value)
                    {
                        current = current.leftChild;
                        if (current == null)
                        {
                            parent.leftChild = newNode;
                            break;
                        }
                    }
                    else
                    {
                        current = current.rightChild;
                        if (current == null)
                        {
                            parent.rightChild = newNode;
                            break;
                        }
                    }
                }
            }
        }

        // 先序遍历
        public static void PreOrderTraverse(Node root)
        {
            if (root != null) //若二叉树为空，则空操作，否则
            {
                root.Display(); // 访问根结点
                PreOrderTraverse(root.leftChild); //先序遍历左子树
                PreOrderTraverse(root.rightChild); //先序遍历右子树
            }
        }

        // 中序遍历
        public static void InOrderTraverse(Node root)
        {
            if (root != null) //若二叉树为空，则空操作，否则
            {
                InOrderTraverse(root.leftChild); //中序遍历左子树
                root.Display(); //访问根结点
                InOrderTraverse(root.rightChild); //中序遍历右子树
            }
        }

        // 后序遍历
        public static void PostOrderTraverse(Node root)
        {
            if (root != null) //若二叉树为空，则空操作，否则
            {
                PostOrderTraverse(root.leftChild); //后序遍历左子树
                PostOrderTraverse(root.rightChild); //后序遍历右子树
                root.Display(); //访问根结点
            }
        }
    }

上面代码中，插入结点的代码逻辑可自己定义，你也可以指定一个另外一个结点，把要插入的结点作为其左孩子或右孩子等。这里的插入结点方法比较简单，按照这个方法可以构造一棵二叉排序树，又叫平衡二叉树，其定义为：这棵树或者是一棵空树；或者是具有下列性质的二叉树：（1）若它的左子树不为空，则左子树上所有结点的值均小于它的根结点；（2）若它的右子树不为空，则右子树上所有结点的值均大于它的根结点；（3）它的左、右子树也分别为二叉排序树。

对于三种遍历算法的代码，是按照其定义去写的，由于是递归调用，所以代码异常简洁。理解递归的最好办法是用简单的数据走一遍代码，所以，如果你没能很好地理解，可以采用这个方法去读代码。

下面是main方法中的调用代码，其中包含了构造二叉树的过程：

        static void Main(string[] args)
        {
            BinaryTree myBinaryTree = new BinaryTree();
            myBinaryTree.Insert();
            myBinaryTree.Insert();
            myBinaryTree.Insert();
            myBinaryTree.Insert();
            myBinaryTree.Insert();
            myBinaryTree.Insert();
            myBinaryTree.Insert();

            Console.Write("PreOrder traverse:  ");
            BinaryTree.PreOrderTraverse(myBinaryTree.root);
            Console.WriteLine();// 9 5 3 2 6 7 12
            Console.Write("InOrder traverse:   ");
            BinaryTree.InOrderTraverse(myBinaryTree.root);
            Console.WriteLine();// 2 3 5 6 7 9 12
            Console.Write("PostOrder traverse: ");
            BinaryTree.PostOrderTraverse(myBinaryTree.root);
            Console.WriteLine();// 2 3 7 6 5 12 9

            Console.ReadLine();
        }

这棵二叉排序树共有7个结点组成，按照Insert方法的代码逻辑，其构成了如下的一棵树：

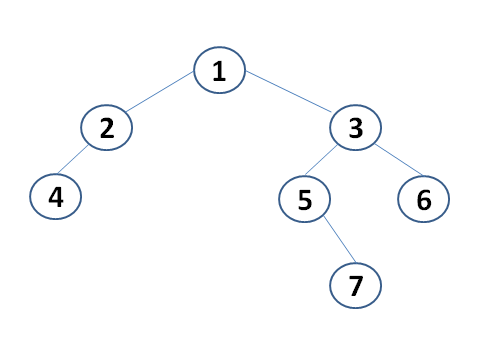
然后分别调用其先序遍历，中序遍历，后序遍历方法，结点输出的顺序应该如下所示：

先序遍历：9 5 3 2 6 7 12

中序遍历：2 3 5 6 7 9 12

后序遍历：2 3 7 6 5 12 9