求出数组前面k个元素或数组中元素大于一半的元素(快速排序与堆排序的灵活运用)
写这个的目的在于,说明快速排序的灵活运用。我们来看下关于快速排序中的一部分关键代码:
int a[101],n;//定义全局变量,这两个变量需要在子函数中使用void quicksort(int left,int right){int i,j,t,temp;if(left>right)return;temp=a[left]; //temp中存的就是基准数i=left;j=right;while(i!=j){//顺序很重要,要先从右边开始找while(a[j]>=temp && i<j)j--;//再找右边的while(a[i]<=temp && i<j)i++;//交换两个数在数组中的位置if(i<j){t=a[i];a[i]=a[j];a[j]=t;}}//最终将基准数归位a[left]=a[i];a[i]=temp;quicksort(left,i-1);//继续处理左边的,这里是一个递归的过程quicksort(i+1,right);//继续处理右边的 ,这里是一个递归的过程}

int partition_quickSort(int *arr,int start,int end){
int cmp_val=arr[start];int i=start;int j=end;while(i!=j){while(i<j&&arr[j]>=cmp_val){j--;}while(i<j&&arr[i]<=cmp_val){i++;}if(i<j){int ex_temp=arr[j];arr[j]=arr[i];arr[i]=ex_temp;}}arr[start]=arr[i];arr[i]=cmp_val;return i;}

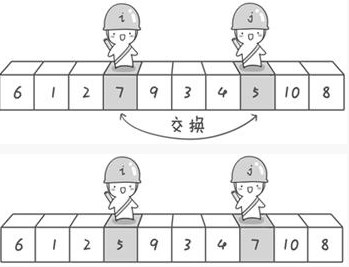
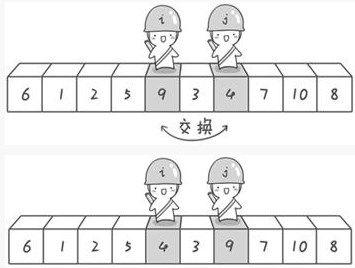

int partition_quickSort(int *arr,int start,int end)

int moreThanHalfNum_Partition(int *arr,int Length){if(arr==NULL||Length==0){return 0;}int low=0;int high=Length-1;int mid=Length>>1;int index= partition_quickSort(arr,low,high);while(index!=mid){if(index>mid){index= partition_quickSort(arr,low,index-1);}else{index= partition_quickSort(arr,index+1,high);}}int key=arr[mid];if(isMoreHalf(arr,Length,key)){return key;}else{return 0;}}
index>mid

index= partition_quickSort(arr,low,index-1);

index= partition_quickSort(arr,index+1,high);

int partition_quickSort(int *arr,int start,int end){int cmp_val=arr[start];int i=start;int j=end;while(i!=j){while(i<j&&arr[j]>=cmp_val){j--;}while(i<j&&arr[i]<=cmp_val){i++;}if(i<j){int ex_temp=arr[j];arr[j]=arr[i];arr[i]=ex_temp;}}arr[start]=arr[i];arr[i]=cmp_val;return i;}
bool minKDataBeforeArr(int *arr,int Length,int k_bef){if(arr==NULL||k_bef>Length){return false;}int start=0;int k_index=0;int end=Length-1;k_index=partition_quickSort(arr,start,end);while(k_index!=k_bef-1){if(k_index>k_bef-1){end=k_index-1;k_index=partition_quickSort(arr,start,end);}else{start=k_index+1;k_index=partition_quickSort(arr,start,end);}}for(int i=0;i<k_bef; i++){for(int j=k_bef;j<Length; j++){if(arr[i]>arr[j]){return false;}}}return true;}
求出数组前面k个元素或数组中元素大于一半的元素(快速排序与堆排序的灵活运用)的更多相关文章
- 使用jQuery匹配文档中所有的li元素,返回一个jQuery对象,然后通过数组下标的方式读取jQuery集合中第1个DOM元素,此时返回的是DOM对象,然后调用DOM属性innerHTML,读取该元素 包含的文本信息
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...
- 从N个元素的集合中随机取m个元素的算法实现
最近有一个需求,比较简单,就是如标题所说的,从N个元素中随机取m个元素,当然这m个元素是不能存在重复的.本以为这么简单的需求,应该有现成的工具类来实现,但是几次查找居然没找到(有知道的可以推荐下哈^_ ...
- Js/Jquery获取iframe中的元素 在Iframe中获取父窗体的元素方法
在web开发中,经常会用到iframe,难免会碰到需要在父窗口中使用iframe中的元素.或者在iframe框架中使用父窗口的元素 js 在父窗口中获取iframe中的元素 1. 格式:window ...
- 定义抽象类Shape,抽象方法为showArea(),求出面积并显示,定义矩形类Rectangle,正方形类Square,圆类 Circle,根据各自的属性,用showArea方法求出各自的面积,在main方法中构造3个对象,调用showArea方法。(体现多态)
实现多态的三个条件:1.要有继承2.要有抽象方法重写3.用父类指针(引用)指向子类对象 重载重写重定义的区别: 1.重载:在同一个类中进行; 编译时根据参数类型和个数决定方法调用; 子类无法重载父类; ...
- 输出数组第k大的元素
用快速排序的思想输出数组第k大的元素: #include<iostream> #include<algorithm> using namespace std; //递归实现:返 ...
- 一个字符串中可能包含a~z中的多个字符,如有重复,如String data="aavzcadfdsfsdhshgWasdfasdf",求出现次数最多的那个字母及次数,如有多个重复的则都求出。
主要掌握String中的方法 char[] toCharArray() 将此字符串转换为一个新的字符数组. int indexOf(String str) 返回 ...
- CSS中伪类及伪元素用法详解
CSS中伪类及伪元素用法详解 伪类的分类及作用: 注:该表引自W3School教程 伪元素的分类及作用: 接下来让博主通过一些生动的实例(之前的作业或小作品)来说明几种常用伪类的用法和效果,其他的 ...
- CSS中2d转换:transition过渡放在:hover伪类中与应用在整个元素中区别
css的2d转换十分强大,能够在不使用js的情况下,实现页面的元素与用户之间更多动态的交互,增强用户体验.其中使用最多的就是hover伪类. 1.创建一个页面的div元素: <!DOCTYPE ...
- 如何求出数组中最小(或者最大)的k个数(least k问题)
输入n个整数,如何求出其中最小的k个数? 解法1. 当然最直观的思路是将数组排序,然后就可以找出其中最小的k个数了,时间复杂度以快速排序为例,是O(nlogn): 解法2. 借助划分(Partitio ...
随机推荐
- reactjs入门到实战(六)---- ReactJS组件API详解
全局的api 1.React.createClass 创建一个组件类,并作出定义.组件实现了 render() 方法,该方法返回一个子级.该子级可能包含很深的子级结构.组件与标准原型类的不同之处在于, ...
- Linux各发行版本简介
简介 Linux 主要作为Linux发行版(通常被称为"distro")的一部分而使用.这些发行版由个人,松散组织的团队,以及商业机构和志愿者组织编写.它们通常包括了其他的系统软件 ...
- JAVA的名词释义
JDK : Java Development Toolkit (java 开发工具包). JDK是整个JAVA的核心,包括了java运行环境(Java Runtime Envirnmet),一堆jav ...
- Bad apple for CSharp
前言:记得10年的时候我还在上学,有一天逛csdn看到了字符版的badapple,感觉这东西好NB啊,然后就下载了一份,最近整理博客就把他整理博客,原作者是谁真心不知道,这是在果壳看到的. Bad A ...
- Eclipse中没有andriod问题解决方法
按照网上教程<andriod+环境搭建_图文版>进行安装android,结果,在eclipse中window->preference下找不到"Android"选项 ...
- C#无需IIS构建XmlRpc服务器
准备 我们使用CookComputing.XmlRpcServerV2 3.0.0来构建XmlRpc服务器. 新建一个控制台项目,在项目中添加对CookComputing.XmlRpcServerV2 ...
- jquery之event与originalEvent的关系、event事件对象用法浅析
在jquery中,最终传入事件处理程序的 event 其实已经被 jQuery 做过标准化处理, 其原有的事件对象则被保存于 event 对象的 originalEvent 属性之中, 每个 even ...
- MyBatis 动态SQL查询,多条件,分页
<?xml version="1.0" encoding="UTF-8"?> <!DOCTYPE mapper PUBLIC "-/ ...
- [poj2785]4 Values whose Sum is 0(hash或二分)
4 Values whose Sum is 0 Time Limit: 15000MS Memory Limit: 228000K Total Submissions: 19322 Accepted: ...
- 输出sed的重定向
默认情况下,sed编辑器会将进步的结果输出到STDOUT上,你可以在shll脚本中使用所有重订向sed编辑器输出的标准方法. 你可以在脚本中用反引号来将sed编辑器命令的输出重定向到一个变量中供后面使 ...
