强化学习算法中log_det_jacobian的影响是否需要考虑

相关：

人形机器人-强化学习算法-PPO算法的实现细节是否会对算法性能有大的影响.

https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch

log_det_jacobian 是什么，我也是头一次遇到，百度了一下，没有答案，Google了一下也没有答案，虽然在TensorFlow的help文档中看到了这个词，但是也没有个适合我的回答，于是我想到了ChatGPT，也是神奇，ChatGPT还真给出了个靠谱的答案。

ChatGPT给出的答案：

应用场景

1. 其用途包括计算概率密度的变换调整，特别是在深度学习中的概率建模和生成模型中，变分推断或生成模型
2. 正态分布的重参数化技巧

从这个回答中可以看到这个log_det_jacobian是计算变量变换时的概率密度计算的，这个log_det_jacobian我是从Google实现PPO的算法代码中看到的，地址：

https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch

接着喝Chatgpt交互，得到：

也就是说我们知道\(x\)变量的概率密度，但是\(y=f(x)\)，也就是说\(y\)是\(x\)的一种变换，那么\(y\)的概率密度就可以通过\(x\)的概率密度计算获得，这里需要知道的是\(x\)变换为\(y\)后并不能保证\(x\)和\(y\)的概率密度是相同的，而是需要使用上面的这个计算公式进行计算的。

根据上面的计算公式可以得到\(y\)的熵和\(x\)的熵之间的关系式：

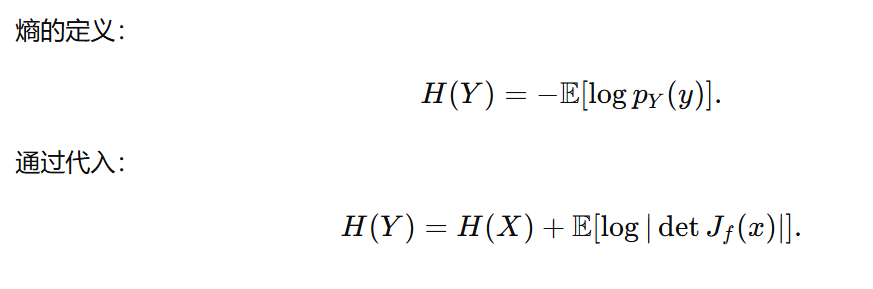
如果\(y=tanh(x)\)，那么可以得到：

需要注意，上面式子中的det可以看做是求导。

因为在https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch中，进行正太分布抽样的action在与环境进行真实交互时进行了变换，即：

  @classmethod
  def dist_postprocess(cls, x):
    return torch.tanh(x)

因此在计算动作的熵的值时进行了log_det_jacobian的计算，具体为：

  @torch.jit.export
  def dist_entropy(self, loc, scale):
    log_normalized = 0.5 * math.log(2 * math.pi) + torch.log(scale)
    entropy = 0.5 + log_normalized
    entropy = entropy * torch.ones_like(loc)
    dist = torch.normal(loc, scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
    entropy = entropy + log_det_jacobian
    return entropy.sum(dim=-1)

其中：

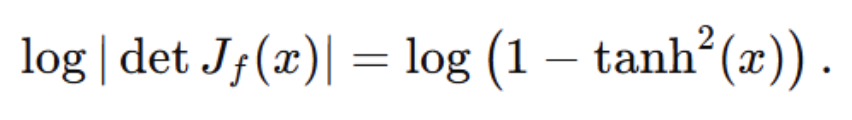
而上面的计算等式等价于：

log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))

关于\(log(1-tanh^2(x))\)和softplus之间的计算这里就不给出了，经过手动演算可以得到等价关系，因此这里通过在计算熵时加入log_det_jacobian从而利用正太分布获得了tanh变换后的熵值。

需要注意的是由于正太分布的熵的计算可以直接通过均值和方差计算而不需要具体的抽样值，而log_det_jacobian的计算需要具体的采样值，因此这里在计算变换后的熵的log_det_jacobian时使用对正态分布进行一次抽样的方法获得\(x\)，从而计算log_det_jacobian，具体为：

    dist = torch.normal(loc, scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))

由此可以看到此种方式计算出的变换后的熵值其实不是一个固定数值，而是一个变量，因为在计算变换后的熵值是采用了对原变量所在分布采样的方式，而按照log_det_jacobian的计算公式的话变换后的熵值也是我们实际应该算的是这个log_det_jacobian的期望值而不是一次抽样。上面代码中dist可以看做是一次抽样，这次的抽样值可以获得（根据正太分布的公式可以计算出概率值），然后根据蒙特卡洛的方式计算出这个真正的log_det_jacobian值期望，也就是上面代码中的log_det_jacobian的期望值，但是这样计算的话需要花费大量的时间，因此上面的代码中只是用一次抽样的值而代替期望值的。

由于熵值的计算其本质就是期望的计算，因素在变量变换后期熵值也应该是log_det_jacobian的期望，但是由于计算的复杂性因此上面采用了一次采样的方式进行替代。但是log_prob的计算是对单次变量变换后的计算，因此不需要计算log_det_jacobian的期望，根据\(y=f(x)=tanh(x)\)的变换时，log_det_jacobian的计算为：

log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))

我们可以得到下面的计算方法：

  @torch.jit.export
  def dist_log_prob(self, loc, scale, dist):
    log_unnormalized = -0.5 * ((dist - loc) / scale).square()
    log_normalized = 0.5 * math.log(2 * math.pi) + torch.log(scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
    log_prob = log_unnormalized - log_normalized - log_det_jacobian
    log_prob = log_unnormalized - log_normalized
    return log_prob.sum(dim=-1)

由此我们在知道\(y=tanh(x)\)，并且\(x\)为正太分布的情况下，我们可以计算出\(y\)估计的熵值，以及\(y\)的log_prob值，由于在这个项目(https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch)中变换后的\(y\)才是真正和环境交互的action，因此我们在PPO算法的计算时需要使用的是\(y\)的熵和log_prob，于是就用了本文对log_det_jacobian的讨论。

在考虑log_det_jacobian的情况下，该项目的PPO算法的性能可以参照：

人形机器人-强化学习算法-PPO算法的实现细节是否会对算法性能有大的影响.

下面给出如果不考虑log_det_jacobian的情况下最终的PPO算法的性能：

-257.35278 626.76746 872.1776 1725.8082 2591.6821 3190.6335 3620.4314 4082.5015 4468.4927 4762.6313 4986.739

-189.53021 588.52185 522.61017 1434.2548 2458.558 3038.153 3335.4653 3691.8052 4317.5156 5113.4204 5509.2427

-176.273 560.4658 743.65686 1602.8649 2622.3098 2960.6648 3334.305 3743.382 4042.1658 4236.974 4528.8677

-197.11514 693.2258 1242.5767 2034.826 2612.6963 2984.8345 3413.858 3686.592 4052.4087 4459.6577 4780.1724

-207.15936 544.1607 698.48737 1465.3678 2158.609 2698.9854 2985.0945 3370.756 3502.2546 3557.984 3639.0762

-247.04488 609.49286 886.9049 1622.353 2578.5637 3369.3296 3897.0066 4506.5947 4957.028 5286.8623 5497.941

-279.18222 695.9527 781.5837 1851.9932 2501.7515 3050.4778 3484.7144 3728.6135 4007.2332 4429.4478 4524.212

-183.95197 539.9428 703.08484 1465.9211 2428.05 2860.103 3250.7612 3718.4924 4047.587 4484.833 4805.9463

-295.8933 576.68585 886.04565 1722.0039 2508.7786 2791.8215 3169.9558 3641.8894 4151.5737 4636.6797 5302.451

-36.912907 599.4662 668.3243 1792.368 2677.549 2945.6028 3446.7866 3810.89 4212.9053 4442.2866 4756.253

-244.0652 518.28076 849.9641 1570.7167 2383.759 2903.143 3339.9314 3587.268 4183.936 4475.66 4758.6304

-202.35239 658.42694 964.961 1996.5828 2911.921 3775.2754 4424.9106 4901.0835 5160.46 5381.5474 5502.6333

-195.47755 727.0509 785.33185 1481.1584 2436.87 2884.1519 3218.7478 3380.975 3832.684 4390.324 4610.152

-181.08733 602.9277 728.14087 1521.0625 2608.9495 3080.9626 3651.573 4102.9014 4449.6143 4698.4717 4890.4004

-238.61224 558.1536 605.8967 1416.7765 2353.3438 3428.1458 4070.3828 4457.718 4998.3643 5468.2817 5891.4756

-238.16461 582.09686 640.10315 1627.2996 2349.885 2821.6912 3364.2283 3956.324 4589.694 4970.996 5397.493

-167.1232 653.3819 1024.1832 1734.4574 2765.6538 3399.1665 4013.0498 4566.583 5195.512 5720.626 6362.57

-535.3739 600.2949 746.9505 1194.6919 2154.8213 2791.384 3152.7737 3470.5764 3652.3142 3722.4675 4133.7183

-163.19084 620.87933 752.57043 1458.3164 2761.9338 3427.4026 4034.8708 4415.851 4773.016 5092.4995 5408.4106

-300.8249 577.7861 658.09735 1257.3555 2249.6567 3033.7153 3471.3848 3659.2483 3870.2793 4178.1357 4606.6177

-166.20488 583.24896 690.0983 1738.1193 2348.6423 2742.8286 3335.221 3890.5684 4799.652 5260.9575 5503.083

-266.85956 619.17346 773.7655 1127.5323 2123.3962 2767.1824 3142.0505 3668.8003 3936.622 4315.424 4624.094

-255.7037 590.5388 696.94073 1876.102 2704.7017 3315.899 3782.566 4320.2144 5016.362 5653.5 6179.2803

-454.73566 578.1404 682.5043 1587.7834 2365.1104 3160.6091 3670.924 4255.612 4715.722 5043.9404 5384.41

-206.27248 563.9714 724.4464 1269.439 2540.5312 3176.687 3653.4167 3972.335 4451.6143 4648.8003 4832.7505

-308.68695 603.69183 765.8216 1611.8046 2448.322 2941.014 3079.1768 3525.0386 3742.15 3821.2664 4372.0264

-130.09026 704.8334 768.9669 1396.059 2249.7283 2820.046 3298.1719 3710.9512 4317.251 4750.7134 5046.205

-204.65765 525.75104 672.4369 1585.34 2550.1016 3051.098 3594.2683 4051.0342 4424.9556 4764.3994 5014.5986

-237.30319 739.284 1051.9974 2056.4387 2696.0054 2955.4573 3486.2598 3918.272 4233.7495 4889.809 5404.9834

-242.54335 621.38965 962.5969 1696.0646 2317.9294 2852.7563 3354.177 3737.5955 4319.241 4802.989 5085.672

-288.39615 556.84576 795.6562 1713.2417 2570.9888 2886.445 3297.397 3614.2622 3870.1985 4135.6274 4407.1704

-429.74948 666.29614 701.57916 1591.0287 2333.2456 2820.5066 3244.6392 3622.8208 3976.641 4385.8735 4972.4155

-275.35324 712.2703 1266.3237 2359.7314 3013.6287 3443.079 3847.1062 4339.8213 4611.9 4782.6143 5023.395

-229.47244 534.31433 753.1219 1044.259 2217.323 2868.86 3312.1223 3389.7986 3984.0874 4299.565 4391.0176

-329.244 576.6534 697.8262 1834.4263 2526.4724 2781.889 3153.1074 3388.3884 3805.649 4069.824 4212.0874

-244.22275 571.94226 859.5749 1827.8851 2615.033 3258.98 3533.412 4008.8008 4581.981 5197.777 5649.0693

-247.01805 695.56165 735.51953 1878.0038 2716.632 3122.833 3684.869 4277.671 4924.1045 5526.931 5993.1846

-273.82922 479.60516 760.0794 1197.3153 2379.7183 3054.5415 3419.6887 3829.669 4269.0845 4609.465 4888.6655

-138.38889 580.5478 687.19836 1491.4299 2319.8115 2890.6023 3392.0647 3958.5054 4562.6865 5192.2983 5572.479

-341.53876 595.2708 701.3693 1794.624 2689.5864 3187.4773 3606.66 3867.8245 4230.921 4435.946 4628.54

可以看到性能结果略有下降，但是从下降的幅度和重复试验的次数来看并不能从数学统计的角度说在分布变换时考虑log_det_jacobian可以提高算法性能，但是如果从计算机research的角度或者说在发paper的角度来说考虑log_det_jacobian是可以提升算法性能的。不过从本文的尝试和实验中可以看到，即使不考虑log_det_jacobian也不会对算法的性能造成明显的下降，但是考虑到考虑log_det_jacobian会更符合数学理论上的解释，因此还是应该尽可能的在变量变换时考虑log_det_jacobian。

个人github博客地址：

https://devilmaycry812839668.github.io/