【POJ】1704 Georgia and Bob（Staircase Nim）

Description

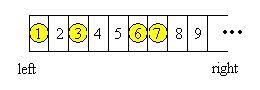
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win
----------------------------------------------------
题意：在一条直线的格子上放有一些棋子，两人可以轮流选择一个棋子向左移动，但不能跨过前面的棋子或到同一个，无法进行操作的人输（即所有棋子都被前后逼死，无法移动）。
分析：可以把两个棋子间的距离看做nim游戏中一堆石子的数量，移动即为取走一些石子，但如果格子上有奇数个棋子，此时无法凑成整堆的石子（即两两棋子算作一堆石子的话，会多出一个棋子），这时把0看做一个棋子即可。注意，题目给的棋子位置不是升序，需要自己排序。
P.s.这种问题也被称作Staircase Nim。

 #include <cstdio>
 #include <algorithm>
 using namespace std;
 int main()
 {
     int t,n,p[];
     scanf("%d",&t);
     while(t--)
     {

         int x=;
         scanf("%d",&n);
         for(int i=;i<n;i++) scanf("%d",&p[i]);
         if(n%!=) p[n++]=;
         sort(p,p+n);
         for(int i=;i<n-;i+=)
         {
             x^=(p[i+]-p[i]-);//不断异或棋子之间的差值，即nim中的石子数
         }
         if(x==) printf("Bob will win\n");
         else  printf("Georgia will win\n");
     }
     return ;
 }

AC了，打卡：【POJ】1704 Georgia and Bob