UE4 坐标系 坐标轴旋转轴
- Pitch是围绕Y轴旋转,也叫做俯仰角。
- Yaw是围绕Z轴旋转,也叫偏航角。
- Roll是围绕X轴旋转,也叫翻滚角。
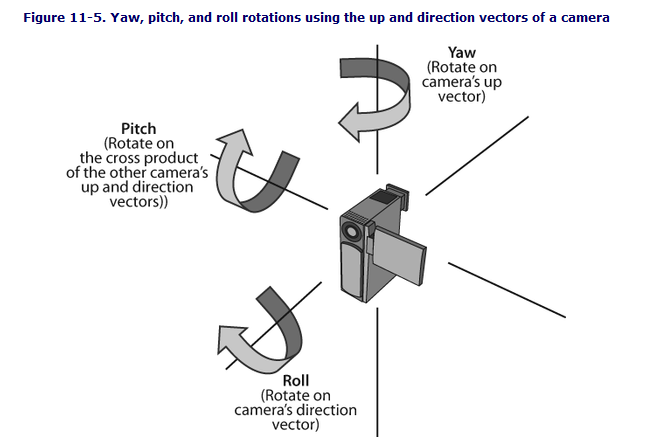
UE4里,蓝图中的rotation的三个依次为roll,pitch,yaw。C++中FRotator里是pitch,yaw,roll。
UE4 坐标系 坐标轴旋转轴的更多相关文章
- Blender下各种坐标系
转载:https://jingyan.baidu.com/article/ed2a5d1f8f018309f7be1779.html 打开blender创建一个立方体. 切换到“自身”坐标系,旋转 ...
- [OpenGL]OpenGL坐标系和坐标变换
OpenGL通过摄像机的模拟.要实现一个三维计算机图形重大转变,这是几何变换(模型转换-查看转型(两者统称为几何变换)).投影.作物转型.口变换等.同一时候,OpenGL还实现了矩阵堆栈等.理解掌握了 ...
- unity还原three之旋转
http://www.360doc.com/content/16/0829/14/12282510_586760119.shtml unity使用左手坐标系,另外在做旋转的时候必须弄清楚旋转坐标轴和旋 ...
- OpenGL基础图形编程
一.OpenGL与3D图形世界1.1.OpenGL使人们进入三维图形世界 我们生活在一个充满三维物体的三维世界中,为了使计算机能精确地再现这些物体,我们必须能在三维空间描绘这些物体.我们又生活在一个充 ...
- 【转】OpenGL基础图形编程(一)
原文:http://blog.chinaunix.net/uid-20638550-id-1909183.html 分类: 一.OpenGL与3D图形世界 1.1.OpenGL使人们进入三维图形世界 ...
- SharpGL学习笔记(七) OpenGL的变换总结
笔者接触OpenGL最大的困难是: 经常调试一份代码时, 屏幕漆黑一片, 也不知道结果对不对,不知道如何是好! 这其实就是关于OpenGL"变换"的基础概念没有掌握好, 以至于对& ...
- OpenGL坐标变换专题
OpenGL坐标变换专题(转) OpenGL通过相机模拟.可以实现计算机图形学中最基本的三维变换,即几何变换.投影变换.裁剪变换.视口变换等,同时,OpenGL还实现了矩阵堆栈等.理解掌握了有关坐 ...
- html5新特性与用法大全了解一下
有好多小伙伴私聊我问我html5新特性 和用法,下面我给大家具体介绍一下html5都新加了哪些新特性,下面我给大家总结一下. 1)新的语义标签 footer header 等等2)增强型表单 表单2. ...
- OpenGL基础图形编程(八)变换
八.OpenGL变换 OpenGL变换是本篇的重点内容,它包含计算机图形学中最主要的三维变换,即几何变换.投影变换.裁剪变换.视口变换,以及针对OpenGL的特殊变换概念理解和使用方法,如相机模拟.矩 ...
随机推荐
- 【设计模式】结构型04桥接模式(Bridge Pattern)
学习地址:http://www.runoob.com/design-pattern/bridge-pattern.html 桥接模式(Bridge Pattern) 桥接模式(Bridge patte ...
- IAR for STM8的简介、下载、安装及注册教程
一.简介 1.关于IAR for STM8 IAR for STM8 是一个嵌入式工作平台,主要应用于STM8 系列芯片的开发,现在(2018年3.10版本)能够支持市面上所有的STM8芯片. 个人认 ...
- vboxnetctl: no such file or directory
 sudo /Library/StartupItems/VirtualBox/VirtualBox restart sudo /Library/StartupItems/VirtualBox/Vir ...
- 如何查看jsplumb.js的API文档(YUIdoc的基本使用)
目录 一.问题描述 二. 处理方法 三. YUIdoc工具介绍 示例代码托管在:http://www.github.com/dashnowords/blogs 博客园地址:<大史住在大前端> ...
- c++学习书籍推荐《深入理解C++11 C++11新特性解析与应用》下载
百度云及其他网盘下载地址:点我 编辑推荐 <深入理解C++11:C++11新特性解析与应用>编辑推荐:C++标准委员会成员和IBM XL编译器中国开发团队共同撰写,权威性毋庸置疑.系统.深 ...
- 【朝花夕拾】Android自定义View篇之(十)TouchSlop及VelocityTracker
前言 在Android事件中,有几个比较基本的概念和知识点需要掌握.比如,表示最小移动阈值的TouchSlop,追踪事件速度的VelocityTracker,用于检测手势的GestureDetecto ...
- bzoj3125: CITY 题解
3125: CITY Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 486 Solved: 213[Submit][Status][Discuss] ...
- 9.16考试 第一题 X国的军队题解
这道题总体来看还是比较满意的.连想带打不超过半个小时,打了不到当时基本读懂后就感觉是贪心,但贪什么很重要,当时一开始想的是贪心死亡人数,从小到大搞,然后自己造了几个小数据,还好WA了,然后又列了一个式 ...
- 【AI】Android Pie中引入的AI功能
前言 “无AI,不未来”,绝对不是一句豪情壮语,AI早已进入到了我们生活当中.去年Google发布的Android Pie系统在AI功能方面就做了重大革新,本文就对Google在新系统中引入的AI功能 ...
- ElasticStack学习(九):深入ElasticSearch搜索之词项、全文本、结构化搜索及相关性算分
一.基于词项与全文的搜索 1.词项 Term(词项)是表达语意的最小单位,搜索和利用统计语言模型进行自然语言处理都需要处理Term. Term的使用说明: 1)Term Level Query:Ter ...
