用Java实现二叉查找树

二叉查找树的实现

1. 原理

　　二叉查找树，又称为二叉排序树、二叉搜索树。对于树中每一个节点X，它的左子树中所有项的值小于X中的项，而它的右子树中所有项的值大于X中的项。二叉查找树的平均深度为O(log N)，搜索元素的时间复杂度也是O(log N)。是两种库集合类TreeSet、TreeMap实现的基础。

2. public API

void makeEmpty( )      --> 置空
boolean isEmpty( )     --> 判空
AnyType findMin( )     --> 寻找最小值
AnyType findMax( )     --> 寻找最大值
boolean contains( x )  --> 是否存在元素x
void insert( x )       --> 插入元素x
void remove( x )       --> 删除元素x
void printTree( )      --> 遍历二叉树

3. 核心思想图解：递归

！寻找最小值

此处用递归实现：

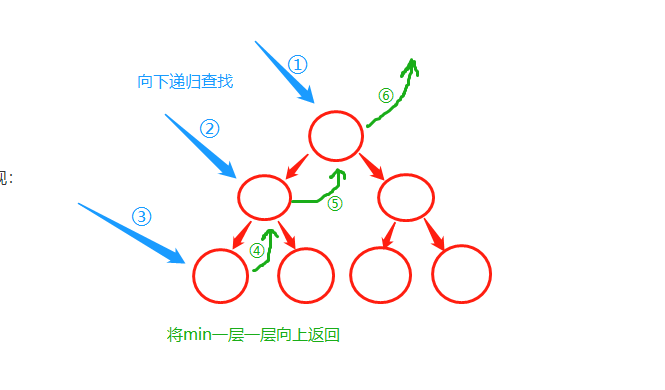
！寻找最大值

此处用非递归实现，也可以用递归实现：

！是否存在元素x

从root开始往下找，找到含有项X的节点，则此操作返回true，没有找到则返回false。

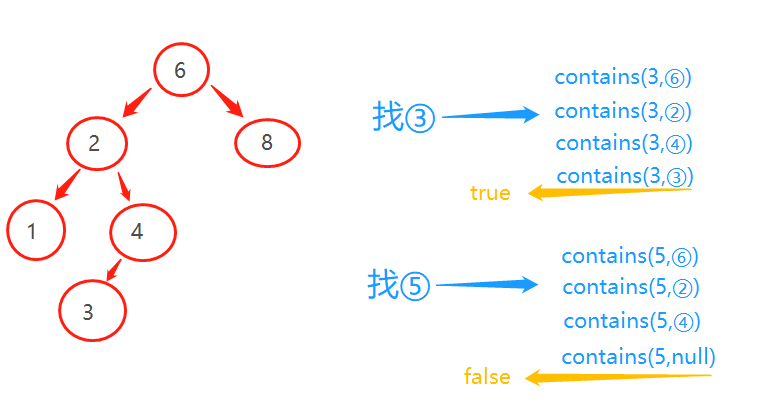
！插入元素x

从root开始往下找到合适的插入位置，然后插入。

！删除元素x

从root开始往下找到元素x，找到则删除，并且处理好后续工作。

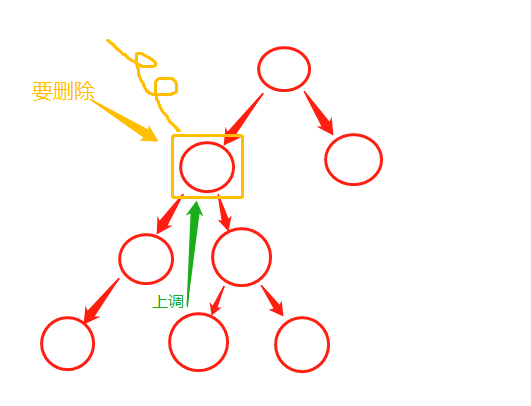
4. BinarySearchTree代码实现

类中，大量使用方法来调用递归方法的技巧，很好地体现了面向对象的封装性。

 /**
  * @author: wenhx
  * @date: Created in 2019/10/8 19:41 （之前）
  * @description: 二叉查找树的实现
  */
 public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {
 ​
     /**
      * 树的根节点
      */
     private BinaryNode<AnyType> root;
 ​
     /**
      * 定义树的节点（内部类）
      */
     private static class BinaryNode<AnyType> {
 ​
         AnyType element;            // 元素值
         BinaryNode<AnyType> left;   // 左孩子
         BinaryNode<AnyType> right;  // 右孩子
 ​
         // 节点的构造器：初始化一个树的节点
         BinaryNode(AnyType theElement) {
             this(theElement, null, null);
         }
 ​
         BinaryNode(AnyType theElement, BinaryNode<AnyType> lt, BinaryNode<AnyType> rt) {
             element = theElement;
             left = lt;
             right = rt;
         }
     }
 ​
     /**
      * 二叉排序树的构造器：初始化根节点
      */
     public BinarySearchTree() {
         root = null;
     }
 ​
     /**
      * 置空
      */
     public void makeEmpty() {
         root = null;
     }
 ​
     /**
      * 判空
      */
     public boolean isEmpty() {
         return root == null;
     }
 ​
     /**
      * 寻找最小值
      */
     public AnyType findMin() {
         if (isEmpty()) {
             throw new RuntimeException();
         }
         return findMin(root).element;
     }
 ​
     /**
      * 寻找最大值
      */
     public AnyType findMax() {
         if (isEmpty()) {
             throw new RuntimeException();
         }
         return findMax(root).element;
     }
 ​
 ​
     /**
      * 是否存在元素x
      */
     public boolean contains(AnyType x) {
         return contains(x, root);
     }
 ​
     /**
      * 插入元素x
      */
     public void insert(AnyType x) {
         root = insert(x, root);
     }
 ​
     /**
      * 删除元素x
      */
     public void remove(AnyType x) {
         root = remove(x, root);
     }
 ​
     /**
      * 遍历此二叉树
      */
     public void printTree() {
         if (isEmpty()) {
             System.out.println("Empty tree");
         } else {
             printTree(root);
         }
     }
 ​
     /**
      * 寻找最小值（内部方法）：此处用递归实现
      */
     private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
         if (t == null) {
             return null;
         } else if (t.left == null) {
             return t;
         }
         return findMin(t.left);
     }
 ​
     /**
      * 寻找最大值（内部方法）：此处用非递归实现
      */
     private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t) {
         if (t != null) {
             while (t.right != null) {
                 t = t.right;
             }
         }
         return t;
     }
 ​
     /**
      * 是否存在元素x（内部方法）
      */
     private boolean contains(AnyType x, BinaryNode<AnyType> t) {
         /**
          * 跳出递归的条件
          */
         if (t == null) {
             return false;
         }
 ​
         /**
          * 如果x小于节点值，则递归到左孩子；
          * 如果x大于节点值，则递归到右孩子；
          * 如果x等于节点值，则找到。
          */
         int compareResult = x.compareTo(t.element);
 ​
         if (compareResult < 0) {
             return contains(x, t.left);
         } else if (compareResult > 0) {
             return contains(x, t.right);
         } else {
             return true;
         }
 ​
     }
 ​
     /**
      * 插入元素x（内部方法）
      */
     private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t) {
         /**
          * 跳出递归的条件
          */
         if (t == null) {
             return new BinaryNode<>(x, null, null);
         }
 ​
         /**
          * 如果x小于节点值，则递归到左孩子；
          * 如果x大于节点值，则递归到右孩子；
          * 如果x等于节点值，则说明已有元素x，无需操作。
          */
         int compareResult = x.compareTo(t.element);
 ​
         if (compareResult < 0) {
             t.left = insert(x, t.left);
         } else if (compareResult > 0) {
             t.right = insert(x, t.right);
         } else {
         }
         return t;
 ​
     }
 ​
     /**
      * 删除元素x（内部方法）
      */
     private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t) {
         /**
          * 跳出递归的条件
          */
         if (t == null) {
             return t;   // Item not found; do nothing
         }
 ​
         /**
          * 如果x小于节点值，则递归到左孩子；
          * 如果x大于节点值，则递归到右孩子；
          * 如果x等于节点值，则要删除此节点。
          */
         int compareResult = x.compareTo(t.element);
 ​
         if (compareResult < 0) {
             t.left = remove(x, t.left);
         } else if (compareResult > 0) {
             t.right = remove(x, t.right);
         } else if (t.left != null && t.right != null) {
             // 要删除的节点有两个孩子（可选用右孩子最小元素/左孩子最大元素上调）
             t.element = findMin(t.right).element;
             t.right = remove(t.element, t.right);
         } else {
             // 要删除的节点有一个孩子或者没有孩子
             t = (t.left != null) ? t.left : t.right;
         }
         return t;
     }
 ​
     /**
      * 遍历此二叉树（内部方法）
      */
     private void printTree(BinaryNode<AnyType> t) {
         // 中序遍历-->即递增顺序
         if (t != null) {
             printTree(t.left);
             System.out.println(t.element);
             printTree(t.right);
         }
     }
 ​
     /**
      * 求树的深度（内部方法）
      */
     private int height(BinaryNode<AnyType> t) {
         if (t == null) {
             return -1;
         } else {
             return 1 + Math.max(height(t.left), height(t.right));
         }
     }
 ​
     /**
      * 主方法用来测试
      */
     public static void main(String[] args) {
         BinarySearchTree<Integer> t = new BinarySearchTree<>();
         t.insert(6);
         t.insert(3);
         t.insert(9);
         t.insert(2);
         t.insert(5);
         t.insert(8);
         t.insert(10);
         t.printTree();
         t.insert(4);
     }
 }

okay，今天就到这啦，一定要掌握这种数据结构哈，真的很重要！！！