numpy+sklearn 手动实现逻辑回归【Python】

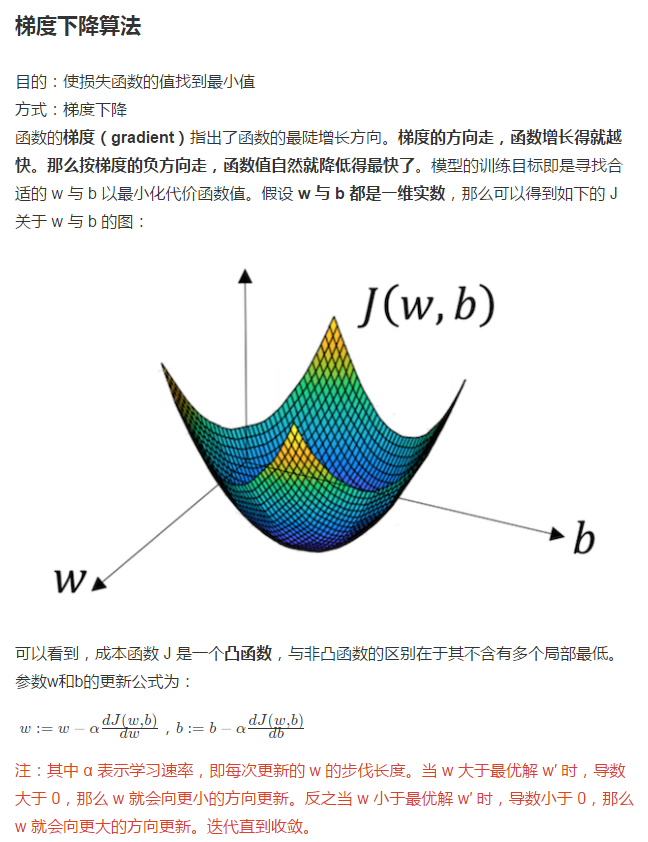
逻辑回归损失函数：

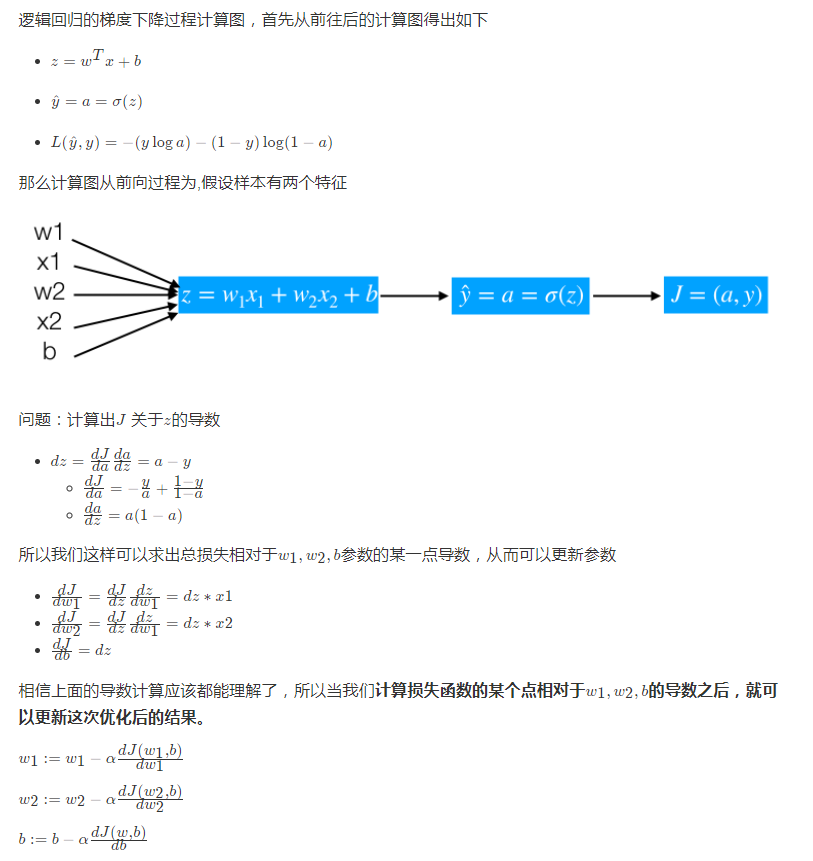
from sklearn.datasets import load_iris,make_classification
from sklearn.model_selection import train_test_split
import tensorflow as tf
import numpy as np

X,Y = make_classification(n_samples=1000,n_features=5,n_classes=2)
x_train,x_test,y_train,y_test = train_test_split(X,Y,test_size=0.3)

def initialize_with_zeros(shape):
    """
    创建一个形状为 (shape, 1) 的w参数和b=0.
    return:w, b
    """
    w = np.zeros((shape, 1))
    b = 0
    return w, b

def basic_sigmoid(x):
    """
    计算sigmoid函数
    """

    s = 1 / (1 + np.exp(-x))

    return s

def propagate(w, b, X, Y):
    """
    参数：w,b,X,Y：网络参数和数据
    Return:
    损失cost、参数W的梯度dw、参数b的梯度db
    """
    m = X.shape[1]

    # w (n,1), x (n, m)
    A = basic_sigmoid(np.dot(w.T, X) + b)
    # 计算损失
    cost = -1 / m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
    dz = A - Y
    dw = 1 / m * np.dot(X, dz.T)
    db = 1 / m * np.sum(dz)
    cost = np.squeeze(cost) # 从数组的形状中删除单维条目，即把shape中为1的维度去掉
    grads = {"dw": dw,
             "db": db}

    return grads, cost

def optimize(w, b, X, Y, num_iterations, learning_rate):
    """
    参数：
    w:权重,b:偏置,X特征,Y目标值,num_iterations总迭代次数,learning_rate学习率
    Returns:
    params:更新后的参数字典
    grads:梯度
    costs:损失结果
    """

    costs = []

    for i in range(num_iterations):

        # 梯度更新计算函数
        grads, cost = propagate(w, b, X, Y)

        # 取出两个部分参数的梯度
        dw = grads['dw']
        db = grads['db']

        # 按照梯度下降公式去计算
        w = w - learning_rate * dw
        b = b - learning_rate * db

        if i % 100 == 0:
            costs.append(cost)
        if i % 100 == 0:
            print("损失结果 %i: %f" %(i, cost))
            print(b)

    params = {"w": w,
              "b": b}

    grads = {"dw": dw,
             "db": db}

    return params, grads, costs

def predict(w, b, X):
    '''
    利用训练好的参数预测
    return：预测结果
    '''

    m = X.shape[1]
    y_prediction = np.zeros((1, m))
    w = w.reshape(X.shape[0], 1)

    # 计算结果
    A = basic_sigmoid(np.dot(w.T, X) + b)

    for i in range(A.shape[1]):

        if A[0, i] <= 0.5:
            y_prediction[0, i] = 0
        else:
            y_prediction[0, i] = 1

    return y_prediction

def model(x_train, y_train, x_test, y_test, num_iterations=2000, learning_rate=0.0001):
    """
    """

    # 修改数据形状
    x_train = x_train.reshape(-1, x_train.shape[0])
    x_test = x_test.reshape(-1, x_test.shape[0])
    y_train = y_train.reshape(1, y_train.shape[0])
    y_test = y_test.reshape(1, y_test.shape[0])
    print(x_train.shape)
    print(x_test.shape)
    print(y_train.shape)
    print(y_test.shape)

    # 1、初始化参数
    w, b = initialize_with_zeros(x_train.shape[0])

    # 2、梯度下降
    # params:更新后的网络参数
    # grads:最后一次梯度(下降损失)
    # costs:每次更新的损失列表
    params, grads, costs = optimize(w, b, x_train, y_train, num_iterations, learning_rate)

    # 获取训练的参数
    # 预测结果
    w = params['w']
    b = params['b']
    y_prediction_train = predict(w, b, x_train)
    y_prediction_test = predict(w, b, x_test)

    # 打印准确率
    print("训练集准确率: {} ".format(100 - np.mean(np.abs(y_prediction_train - y_train)) * 100))
    print("测试集准确率: {} ".format(100 - np.mean(np.abs(y_prediction_test - y_test)) * 100))

    return None

if __name__ == '__main__':
    model(x_train, y_train, x_test, y_test, num_iterations=500, learning_rate=0.01)