JavaScript图形实例：窗花图案

1．窗花基本框线

设定曲线的坐标方程为：

n=25;

r=100;

x=r/n*cos(5*θ)+r*cos(θ);

y=r/n*sin(5*θ)+r*sin(θ); （0≤θ≤2π）

编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>窗花基本框线</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="blue";

context.lineWidth=2;

context.beginPath();

var n=25;

var r=100;

for (theta=0;theta<=2*Math.PI;theta+=Math.PI/180)

{

x=150+r/n*Math.cos(5*theta)+r*Math.cos(theta);

y=150+r/n*Math.sin(5*theta)+r*Math.sin(theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出如图1所示的一条闭合曲线。

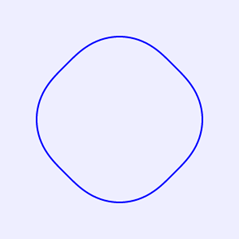
图1 n=25，r=100时的闭合曲线

上述代码中，参数n和r可以根据需要进行设置，r的含义相当于闭合曲线的半径（实际的闭合曲线半径会比r大一些），r/n的比值给定闭合曲线的平滑度，r/n越大，闭合曲线的旋结越大。例如，n=5，r=100时绘制的闭合曲线如图2所示。n=2，r=100时绘制的闭合曲线如图3所示。

图2 n=5，r=100时的闭合曲线

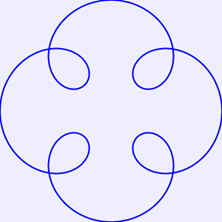
图3 n=2，r=100时的闭合曲线

2．简单的窗花图案

我们采用图1所示的闭合曲线作为外框线，图3所示的闭合曲线作为内部图案线（r值需要适当减小，使得绘制的曲线不会超出外框线），可以绘制出简单的窗花图案。编写的HTML文件内容如下。

<!DOCTYPE html>

<head>

<title>简单的窗花图案</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="blue";

context.lineWidth=2;

context.beginPath();

var n=25;

var r=100;

for (theta=0;theta<=2*Math.PI;theta+=Math.PI/180)

{

x=150+r/n*Math.cos(5*theta)+r*Math.cos(theta);

y=150+r/n*Math.sin(5*theta)+r*Math.sin(theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

var n=2;

var r=50;

for (theta=0;theta<=2*Math.PI;theta+=Math.PI/180)

{

x=150+r/n*Math.cos(5*theta)+r*Math.cos(theta);

y=150+r/n*Math.sin(5*theta)+r*Math.sin(theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出简单的窗花图案，如图4所示。

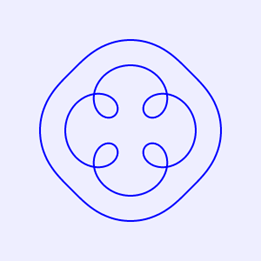
图4 简单的窗花图案

3．精美的窗花图案

在上面程序的基础上，我们编写如下的HTML文件，可以绘制出更精美的窗花图案。

<!DOCTYPE html>

<head>

<title>精美的窗花图案</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="blue";

context.lineWidth=2;

context.beginPath();

var n=25;

for (r=100;r<=115;r+=5)

for (theta=0;theta<=2*Math.PI;theta+=Math.PI/180)

{

x=150+r/n*Math.cos(5*theta)+r*Math.cos(theta);

y=150+r/n*Math.sin(5*theta)+r*Math.sin(theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

var r=45;

for (n=1;n<=4;n++)

for (theta=0;theta<=2*Math.PI;theta+=Math.PI/180)

{

x=150+r/n*Math.cos(5*theta)+r*Math.cos(theta);

y=150+r/n*Math.sin(5*theta)+r*Math.sin(theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出精美的窗花图案，如图5所示。

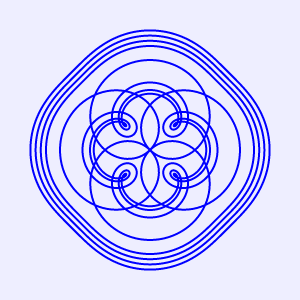
图5 精美的窗花图案