最小生成树（Kruskal算法-边集数组）

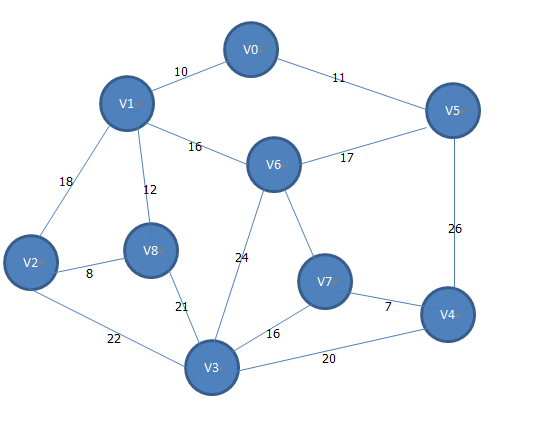
以此图为例：

package com.datastruct;

import java.util.Scanner;

public class TestKruskal {

    private static class Edge{
        public Edge(int begin,int end,int weight){
            this.begin = begin;
            this.end = end;
            this.weight = weight;
        }

        int begin;
        int end;
        int weight;

        public String toString() {
            return "("+begin+", "+end+") -> "+weight;
        }
    }

    private static class Mgraph{
        final int MAXEDGE = ; //最大边数
        final int MAXVEX = ;  //最大顶点数
        int numEdges;
        int numVertexes;
        String vexs[] = new String[MAXVEX]; //顶点数组
        Edge edges[] = new Edge[MAXEDGE]; //边集数组

    }

    public static void CreateMGraph(Mgraph g){
        int i;
        Scanner scanner = new Scanner(System.in);

        System.out.println("输入 顶点数 和边数 ");
        g.numVertexes = scanner.nextInt();
        g.numEdges = scanner.nextInt();

        System.out.println("输入全部顶点：");
        for(i=;i<g.numVertexes;i++){
            g.vexs[i] = scanner.next();
        }

        for(i=;i<g.numEdges;i++){
            System.out.println("输入边 begin end weight ");
            int begin = scanner.nextInt();
            int end = scanner.nextInt();
            int weight = scanner.nextInt();

            g.edges[i] = new Edge(begin,end,weight);

        }

    }

    public static void print(Mgraph g){
        int i;
        System.out.println("所有顶点：");
        for(i=;i<g.numVertexes;i++){
            System.out.print(" "+g.vexs[i]);
        }

        System.out.println("\n所有边：");
        for(i=;i<g.numEdges;i++){
            System.out.println(g.edges[i].toString());
        }

    }

    public static int Find(int parent[], int f){
        while(parent[f] > ){
            f = parent[f];
        }
        return f;

    }

    public static void sortByWeight(Mgraph g){

         Edge temp;
         int i,j;
         boolean flag = true;
         for(i=;i<g.numEdges- && flag;i++){
             flag = false;
             for(j=g.numEdges-;j>=i;j--){
                 if(g.edges[j].weight > g.edges[j+].weight){

                     temp= g.edges[j];
                     g.edges[j] = g.edges[j+];
                     g.edges[j+] = temp;

                     flag = true;
                 }
             }
         }

    }
    public static void MiniSpanTree_Kruskal(Mgraph g){

        sortByWeight(g);//先根据权值从小到大排序

        int i,j,n,m;

        Edge edge[] = g.edges;
        int parent[] = new int[g.MAXVEX];

        for(i=;i<g.numVertexes;i++){
            parent[i] = ;
        }
        System.out.println("最小生成树：");
        for(i=;i<g.numEdges;i++){
            n = Find(parent,edge[i].begin);
            m = Find(parent,edge[i].end);
            if(n != m){
                parent[n] = m;
                System.out.println(edge[i].toString());
            }

        }

    }

    public static void main(String[] args) {
        Mgraph g = new Mgraph();
        CreateMGraph(g); // 创建图，边集数组形式
        print(g); //打印图的基本信息

        MiniSpanTree_Kruskal(g); //找到最小生成树

    }

}