MCMC&Gibbs sampling
Note of Markov Chain Monte Carlo and Gibbs Sampling : http://pan.baidu.com/s/1jHpWY1o
序:A major limitation towards more widespread implementation of Bayesian approaches is that obtaining thee posterior distribution often requires the integration of high-dimensional functions. Here the MCMC is used to solve this problem. There are two major method in the using of MCMC ---- Metropolis algorithm and Gibbs sampling.
- Monte Carlo Integration
问题:计算一个复杂积分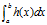
解决方案:把 分解成
分解成 和
和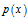 ,要求
,要求 是概率密度函数,得到
是概率密度函数,得到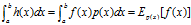 ,将函数积分转换为随机变量函数的期望进行计算。
,将函数积分转换为随机变量函数的期望进行计算。 ,这里的xi是服从概率分布密度为
,这里的xi是服从概率分布密度为 的随机变量x的取值。
的随机变量x的取值。
应用在贝叶斯理论中,后验概率 。
。
- Introduction to Markov Chain
介绍了马尔科夫过程,马尔可夫链,状态空间,转移概率,转移矩阵,以及切普曼-柯尔莫哥洛夫方程,平稳分布等概念。这里提及了从离散的平稳分布向连续状态进行过渡: à
à
- The Metropolis-Hasting Algorithm
问题:从复杂的概率分布p(x)中采样。
解决方案:假如我们要从p(x)=f(x)/K中采样,但是K 并不已知且无法求取,则采取如下方法进行采样
a.设定初始值x0,要满足f(x0)>0;
b.利用现在的x值,从转移分布q(x1,x2)中采样一个候选参数x*,对这个转移分布的限制是q(x1,x2)=q(x2,x1);
c.计算 (这里用的是比值所以可以避开K 进行计算);
(这里用的是比值所以可以避开K 进行计算);
d.如果alpha大于1则接受候选 x*;如果alpha小于1,则以概率alpha接受候选x*;然后返回到步骤b.
4. The Gibbs Sampler
这种采样方法应用在多变量的分布当中,在采样时,我们每次只对一个变量进行采样将其他变量固定。也就是说每次都是对一个单变量的条件分布进行采样,而不去理会联合分布,这样对n个变量进行轮流采样,进行k轮之后得到一个长度为k 的Gibbs Sequence 用来表示联合分布的采样。文章中的Example 4里列出了一个二维的联合分布的采样过程,他的两个条件分布分别为二项分布和Beta分布,很好的诠释 了Gibbs采样的流程和优势。
另外,这里还比较了吉布斯采样和EM算法的联系与区别。
EM每次都包含两个步骤:a.在固定参数下对隐变量求期望;b.固定隐变量的取值,利用极大似然的方法对参数数进行估计。
吉布斯采样则将隐变量和参数看成同等地位进行随机采样,可以看成是对EM算法的随机模拟。(原文:The Gibbs sampler can be thought of as a stochastic analog to the EM approaches used to obtain likelihood functions when missing data are present .)
参考:《统计学习方法》;
《Pattern recognition and machine learning 》第十一章 .
MCMC&Gibbs sampling的更多相关文章
- MCMC,GIBBS SAMPLING简单摘要
本文后面很多内容都是参考博客:http://www.cnblogs.com/xbinworld/p/4266146.html.本文主要用作学习交流备忘用. 1)简述: 随机模拟也可以叫做蒙特卡洛模拟, ...
- 随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- 机器学习方法(八):随机采样方法整理(MCMC、Gibbs Sampling等)
转载请注明出处:Bin的专栏,http://blog.csdn.net/xbinworld 本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比 ...
- 随机采样方法整理与讲解(Acceptance-Rejection、MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- 随机模拟MCMC和Gibbs Sampling
随机模拟 统计模拟中有一个重要的问题就是给定一个概率分布 p(x),我们如何在计算机中生成它的样本.一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的. 通过线性同余发生器可以生成伪随机 ...
- 【转载】MCMC和Gibbs Sampling算法
转载随笔,原贴地址:MCMC和Gibbs Sampling算法 本文是整理网上的几篇博客和论文所得出来的,所有的原文连接都在文末. 在科学研究中,如何生成服从某个概率分布的样本是一个重要的问题.如果样 ...
- LDA-math-MCMC 和 Gibbs Sampling
http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/ 3.1 随机模拟 随机模拟(或者统计模拟)方法有一个很酷的别名是蒙特卡罗方法(Mon ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling
http://blog.csdn.net/pipisorry/article/details/51373090 吉布斯采样算法详解 为什么要用吉布斯采样 通俗解释一下什么是sampling. samp ...
随机推荐
- jsp页面获取当前系统时间
value="<% out.print(new java.text.SimpleDateFormat("yyyy-MM-dd hh:mm:ss").format(n ...
- 百度DMA+小度App的蓝牙语音解决方案技术难点解析
前记 你平时在商场看到的语音助手,看起来非常的简单,其实,这个小小语音助手的背后,是一个非常的复杂的技术支撑.从前端到后端的技术依次是:前端语音降噪技术,高效的音频编解码技术,蓝牙双模技术,DMA ...
- 使用SonarQube+Eclipse来分析python代码
背景 最近在项目中推广集成测试的理念以及相关工具,在jenkins中集成sonar去分析项目的java代码的时候,意外的发现,sonarqube上还有对应python的插件,而自己写的测试工具大部分都 ...
- $51nod\ 1522$ 上下序列 $dp$
正解:$dp$ 解题报告: 传送门$QwQ$ 一年过去了$gql$还是不咋会这题,,,好菜昂我的$NOIp$必将惨败了$kk$ 考虑从大到小枚举两个相同的数填哪儿,根据那个限制,十分显然的是这两个数必 ...
- 洛谷$P1864\ [NOI2009]$二叉查找树 区间$dp$
正解:区间$dp$ 解题报告: 传送门$QwQ$ 首先根据二叉查找树的定义可知,数据确定了,这棵树的中序遍历就已经改变了,唯一能改变的就是通过改变权值从而改变结点的深度. 发现这里权值的值没有意义,所 ...
- 1074 宇宙无敌加法器 (20分)C语言
地球人习惯使用十进制数,并且默认一个数字的每一位都是十进制的.而在 PAT 星人开挂的世界里,每个数字的每一位都是不同进制的,这种神奇的数字称为"PAT数".每个 PAT 星人都必 ...
- ipaclient 4.5.4 requires jinja2, which is not installed. rtslib-fb 2.1.63 has requirement pyudev>=0.16.1, but you'll have pyudev 0.15 which is incompatible. ipapython 4.5.4 has requirement dnspython>=
- 【转】C#中base关键字的几种用法:base()
转:https://blog.csdn.net/cplvfx/article/details/82982862 base其实最大的使用地方在面相对象开发的多态性上,base可以完成创建派生类实例时调用 ...
- [Windows] 系统清理与优化神器Advanced SystemCare 13 PRO非破解附正版激活码
Advanced SystemCare是一款功能强大的系统清理优化软件,该软件提供的主要功能有:启动项优化.注册表整理和清理.隐私清扫.垃圾文件清理.快捷方式修复.恶意软件清除.网络加速.系统优化.安 ...
- 【原创】快速失败机制&失败安全机制
这是why技术的第29篇原创文章 之前在写<这道Java基础题真的有坑!我求求你,认真思考后再回答.>这篇文章时,我在8.1小节提到了快速失败和失败安全机制. 但是我发现当我搜索" ...
