2331: [SCOI2011]地板 插头DP

国际惯例的题面: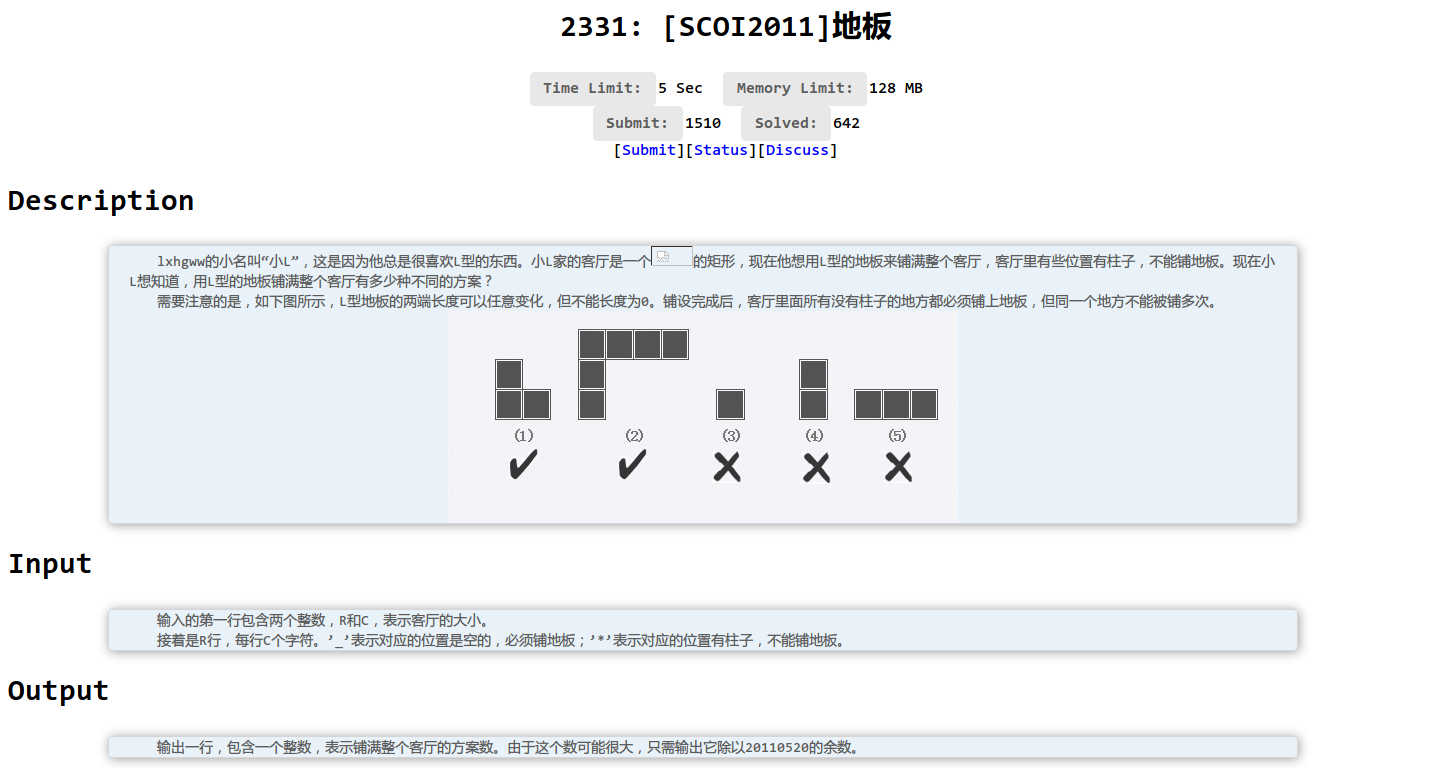

十分显然的插头DP。由于R*C<=100，所以min(R,C)<=10，然后就可以愉悦地状压啦。
我们用三进制状压，0表示没有插头，1表示有一个必须延伸至少一格且拐弯的插头，2表示有一个必须延伸一格且不可以拐弯的插头。
转移的话就十分显然了。
00->22，表示用这个格子作为开始的拐角。
00->10，表示用这个格子向下延伸。
00->01，表示用这个格子向右延伸。
01->10，表示这个格子连接上下。
01->02，表示在这个格子作为中间的拐角。
02->20，表示这个格子连接上下。
02->00，表示这个格子作为某个地板的终点。
10->01，表示这个格子连接左右。
10->20，表示在这个格子作为中间的拐角。
11->00，表示这个格子作为结束的拐角。
20->00，表示这个格子作为某个地板的终点。
20->02，表示这个格子连接左右。
(插头DP的本质就是分类讨论，所以麻烦也没办法，想明白就很容易了)
然后就是实现了。我是用unordered_map存储状态，同时先找到第一个可以放东西的位置开始DP，统计答案的时候统计第n+1行没有插头的状态。

代码:

 #pragma GCC optimize(2)
 #include<cstdio>
 #include<cstring>
 #include<tr1/unordered_map>
 using namespace std;
 using namespace tr1;
 const int maxn=1e2+1e2;
 const int mod=;

 int sta[maxn],nxt[maxn];
 char in[maxn][maxn]; // in == 1 means empty .
 int n,m,cur,fx,fy;
 unordered_map<int,int> f[];

 inline void unzip(int* sta,int ss) {
     for(int i=m+;i;i--) sta[i] = ss %  , ss /= ;
 }
 inline int zip(int* sta) {
     int ret = ;
     for(int i=;i<=m+;i++) ret = ret *  + sta[i];
     return ret;
 }

 inline void core_trans(unordered_map<int,int> &dst,int x,int y,int add) {
     memcpy(nxt,sta,sizeof(int)*(m+));
     if( !in[x][y] ) { // not empty .
         if( sta[y] ==  && sta[y+] ==  ) ( dst[zip(nxt)] += add ) %= mod;
         return;
     }
     if( sta[y] ==  ) {
         if( sta[y+] ==  ) {
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
         } else if( sta[y+] ==  ) {
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
         } else if( sta[y+] ==  ) {
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
         }
     } else if( sta[y] ==  ) {
         if( sta[y+] ==  ) {
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
         } else if( sta[y+] ==  ) nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
     } else if( sta[y] ==  ) {
         if( sta[y+] ==  ) {
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
             nxt[y] =  , nxt[y+] =  , ( dst[zip(nxt)] += add ) %= mod;
         }
     }
 }
 inline void trans(const unordered_map<int,int> &sou,unordered_map<int,int> &dst,int x,int y) {
     dst.clear();
     for(unordered_map<int,int>::const_iterator it=sou.begin();it!=sou.end();it++) if( it->second ) {
         unzip(sta,it->first) , core_trans(dst,x,y,it->second);
     }
 }
 inline void transline(const unordered_map<int,int> &sou,unordered_map<int,int> &dst) {
     dst.clear();
     for(unordered_map<int,int>::const_iterator it=sou.begin();it!=sou.end();it++) if( it->second && ! ( it->first %  ) ) {
         dst[it->first/] = it->second;
     }
 }

 inline void revert() { // make m <= n .
     static char tp[maxn][maxn];
     memcpy(tp,in,sizeof(in)) , memset(in,,sizeof(in));
     for(int i=;i<=n;i++) for(int j=;j<=m;j++) in[j][i] = tp[i][j];
     swap(n,m);
 }

 int main() {
     scanf("%d%d",&n,&m) , fx = - , fy = -;
     for(int i=;i<=n;i++) {
         scanf("%s",in[i]+);
         for(int j=;j<=m;j++) in[i][j] = in[i][j] == '_';
     }

     if( n < m ) revert();
     for(int i=;i<=n&&!~fx;i++) for(int j=;j<=m&&!~fx;j++) if(in[i][j]) fx = i , fy = j;
     if( !~fx ) return puts("") , ; // nothing to do .
     sta[fy] =  , sta[fy+] =  , f[cur][zip(sta)] = ;
     sta[fy] =  , sta[fy+] =  , f[cur][zip(sta)] = ;
     sta[fy] = sta[fy+] =  , f[cur][zip(sta)] = ;
     for(int j=fy+;j<=m;j++) trans(f[cur],f[cur^],fx,j) , cur ^= ;
     transline(f[cur],f[cur^]) , cur ^= ;

     for(int i=fx+;i<=n;i++) {
         for(int j=;j<=m;j++)
             trans(f[cur],f[cur^],i,j) , cur ^= ;
         transline(f[cur],f[cur^]) , cur ^= ;
     }

     printf("%d\n",f[cur][]);

     return ;
 }

たいせつなきみのために ぼくにできるいちばんのことは
为了最重要的你 我所能做的最好的事
約束を忘れること君への想い消し去ること
就是忘却与你的约定抹去对你的思念
沈む夕日暮れてく空 夜の帳舞い降りる頃
渐渐归隐大地的夕阳 夜幕降临整个天空 夜的气息轻盈飘落之时
僕は目を閉じて それは闇に溶けるように 滲んで消えた
我闭目去感受 一切就像溶入暗影一样 渗透进去消散无痕了

未来なんていらないよ
未来（明日）什么的已经不需要了吧
君が側にいる過去のままで
因为有你一直陪伴我的往昔（昨日）