集成学习一: Bagging

偏倚与方差
Bagging
参考文献:

''团结就是力量''

对问题进行建模时, 算法无论如何优化都无法达到我们的要求,又或者精准算法的实现或调优成本太大, 这时,我们就会想,能不能把几个算法或模型结合起来,以'集体'的力量来解决问题? 这就是集成学习产生的原因.

偏倚与方差

在俱体讲解集成学习之前,先介绍一个概念偏倚-方差.

衡量模型的好坏, 最常用的方法就是其准确性, 拿回归举例, 数据真实值是 y, 而我们应用某一模型预测到的值是 \(\hat{y}\). 那误差率可以很容易的表示成:
\[
\begin{array}\\
E[error] &=& E[(\hat{y} - y)^2]\\
&=& E[(\hat{y} - \bar{y} + \bar{y} - y)^2] \\
&=& E[(\hat{y}-y)^2 -2(\hat{y}-\bar{y})(\bar{y}-y)+(\bar{y}-y)^2]\\
&=& E[(\hat{y}-\bar{y})^2 ]+E[(\bar{y}-y)^2]
\end{array}
\]
其中\(\bar{y}\) 是 \(\hat{y}\) 的期望, 前一项是预测值与期望的差别, 即方差(variance), 后一项是预测期望与真实值的差别, 即偏差(bias 或\(bias^2\)定义不同而已). 这就是所谓的偏倚-方差分解(Bias-variance decomposition, BVD).

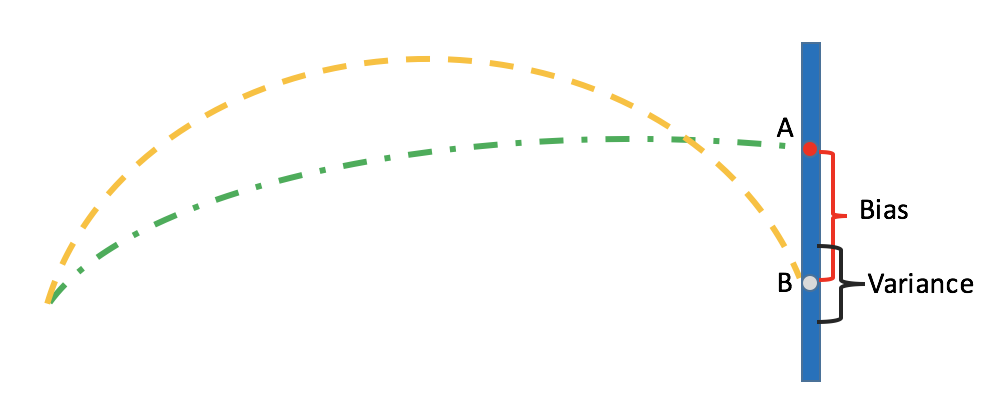
如上图示, 比如靶点在 A 位置, 可是某人的射击落点却总在B点附近, 这时B点可以当作是此人的射击位置期望, BVD中的偏倚与方差如图标示.

因此误差率可表示为:
\[
error = b + v+ \epsilon^2
\]
其中\(\epsilon\) 是噪声.

机器学习的优化, 无非是优化V, D 或者二者. 集成学习主要有两种思路, 一种是Bagging, 一种是boosting, 本质上是对V, D的不同优化方式.

本文来主要介绍下Bagging.

Bagging

Bagging 是并行式集成学习, 也可以说是投票式(voting)式学习. 以少数服从多数的原则来进行表决.

Bagging 是基于自助采样法(bootstrap samplinhg), 是bootstrap aggregating 的合成词.

Bagging算法有两个关键点, 一是自助采样, 二是投票.

自助采样

Bagging是多个学习器组合的集成学习, 每个学习器(称为基学习器) 都要独立训练, 每个基学习器的输入数据是有放回的从样本中抽取子样本(subsampling), 数量一般要求同原样本的数据量(个数) 一致.(ps: 每个个体被抽到的概率是\(1 - (1-\frac{1}{n})^n \approx 63.2\%\))

投票

当每个基学习器训练完成后,对每个个体进行(民主)投票表决, 比如分类, 得票最多的类别即为此个体的类别.

随机森林

随机森林(Random Forest) 也是Bagging 方式, 并且对其进行了改进: 不但对样本进行 subsampling(也称为row subsampling), 而且也对属性进行subsample( 也称column subsampling).

另外提一点的是, 虽然随机森经常以决策树作为基学习器,但从其建模过程来看, 并不局限于此,也就是其他算法作为基分类器也是允许的.

从BVD的角度, bagging 优化的是Variance, 即尽可能的使模型的方差减小, 以达到一个可接受的泛化能力.

参考文献:

机器学习, 2016, 周志华, 清华大学出版社
数据挖掘,2011, Pang-Ning Tan et al, 范明等译, 人民邮电出版社.