机器学习基础知识笔记（一）-- 极大似然估计、高斯混合模型与EM算法

似然函数

常说的概率是指给定参数后，预测即将发生的事件的可能性。拿硬币这个例子来说，我们已知一枚均匀硬币的正反面概率分别是0.5，要预测抛两次硬币，硬币都朝上的概率：

H代表Head，表示头朝上

p(HH | pH = 0.5) = 0.5*0.5 = 0.25.

这种写法其实有点误导，后面的这个p其实是作为参数存在的，而不是一个随机变量，因此不能算作是条件概率，更靠谱的写法应该是 p(HH;p=0.5)。

而似然概率正好与这个过程相反，我们关注的量不再是事件的发生概率，而是已知发生了某些事件，我们希望知道参数应该是多少。

现在我们已经抛了两次硬币，并且知道了结果是两次头朝上，这时候，我希望知道这枚硬币抛出去正面朝上的概率为0.5的概率是多少？正面朝上的概率为0.8的概率是多少？

如果我们希望知道正面朝上概率为0.5的概率，这个东西就叫做似然函数，可以说成是对某一个参数的猜想（p=0.5）的概率，这样表示成(条件)概率就是

L(pH=0.5|HH) = P(HH|pH=0.5) = （另一种写法）P(HH;pH=0.5).

为什么可以写成这样？我觉得可以这样来想：

似然函数本身也是一种概率，我们可以把L(pH=0.5|HH)写成P(pH=0.5|HH); 而根据贝叶斯公式，P(pH=0.5|HH) = P(pH=0.5,HH)/P(HH)；既然HH是已经发生的事件，理所当然P(HH) = 1,所以：

P(pH=0.5|HH)  = P(pH=0.5,HH) = P(HH;pH=0.5).

右边的这个计算我们很熟悉了，就是已知头朝上概率为0.5，求抛两次都是H的概率，即0.5*0.5=0.25。

所以，我们可以safely得到:

L(pH=0.5|HH) = P(HH|pH=0.5) = 0.25.

这个0.25的意思是，在已知抛出两个正面的情况下，pH = 0.5的概率等于0.25。

如果考虑p_H = 0.6，那么似然函数的值也会改变。

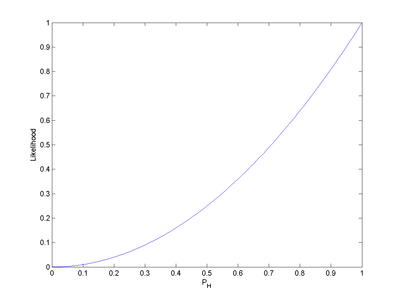
注意到似然函数的值变大了。这说明，如果参数p_H 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设p_H = 0.5时更大。也就是说，参数p_H 取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。

在这个例子中，似然函数实际上等于：

， 其中。

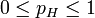如果取p_H = 1，那么似然函数达到最大值1。也就是说，当连续观测到两次正面朝上时，假设硬币投掷时正面朝上的概率为1是最合理的。

类似地，如果观测到的是三次投掷硬币，头两次正面朝上，第三次反面朝上，那么似然函数将会是：

， 其中T表示反面朝上，。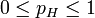

这时候，似然函数的最大值将会在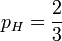的时候取到。也就是说，当观测到三次投掷中前两次正面朝上而后一次反面朝上时，估计硬币投掷时正面朝上的概率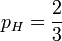是最合理的。

那么最大似然概率的问题也就好理解了。

最大似然概率，就是在已知观测的数据的前提下，找到使得似然概率最大的参数值。

极大似然估计

如果总体X为离散型

假设分布率为P=p(x;θ)P=p(x;θ)，x是发生的样本，θθ是代估计的参数，p(x;θ)p(x;θ)表示估计参数为θθ时，发生x的的概率。

那么当我们的样本值为：x1,x2,...,xnx1,x2,...,xn时，

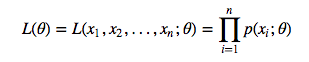
其中L(θ)L(θ)成为样本的似然函数。

假设

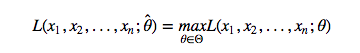
有 θ̂ θ^ 使得 L(θ)L(θ) 的取值最大，那么 θ̂ θ^就叫做参数 θθ 的极大似然估计值。

如果总体X为连续型

基本和上面类似，只是概率密度为f(x;θ)f(x;θ)，替代p。

解法

1. 构造似然函数L(θ)L(θ)
2. 取对数：lnL(θ)lnL(θ)
3. 求导，计算极值
4. 解方程，得到θ

解释一下，其他的步骤很好理解，第二步取对数是为什么呢？

因为根据前面你的似然函数公式，是一堆的数字相乘，这种算法求导会非常麻烦，而取对数是一种很方便的手段：

• 由于ln对数属于单调递增函数，因此不会改变极值点
• 由于对数的计算法则：lnab=blnalnab=blna、lnab=lna+lnblnab=lna+lnb ，求导就很方便了

EM算法

https://blog.csdn.net/zouxy09/article/details/8537620 （讲得很详细）

参考资料：

[1] https://en.wikipedia.org/wiki/Likelihood_function

[2] https://www.cnblogs.com/zhsuiy/p/4822020.html(似然函数)

[3] https://blog.csdn.net/fangbingxiao/article/details/78878141(似然函数)

[4] https://blog.csdn.net/expleeve/article/details/50466602(似然函数)

[5] https://www.cnblogs.com/xing901022/p/8418894.html(极大似然估计法)

[6] https://blog.csdn.net/zouxy09/article/details/8537620(从最大似然到EM算法浅解) 非常好！！！

[7] http://www.cnblogs.com/wjy-lulu/p/7010258.html

[8] http://www.ituring.com.cn/article/497545 (一文详解高斯混合模型原理)

[9] https://blog.csdn.net/jinping_shi/article/details/59613054 (高斯混合模型（GMM）及其EM算法的理解)

[10] http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html (混合高斯模型（Mixtures of Gaussians）和EM算法)

[11] https://blog.csdn.net/jasonzhoujx/article/details/81947663 (高斯混合模型(GMM)应用：分类、密度估计、生成模型)