3.基于梯度的攻击——PGD

PGD攻击原论文地址——https://arxiv.org/pdf/1706.06083.pdf

1.PGD攻击的原理

　　PGD（Project Gradient Descent)攻击是一种迭代攻击，可以看作是FGSM的翻版——K-FGSM (K表示迭代的次数），大概的思路就是，FGSM是仅仅做一次迭代，走一大步，而PGD是做多次迭代，每次走一小步，每次迭代都会将扰动clip到规定范围内。

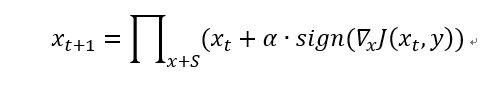
一般来说，PGD的攻击效果比FGSM要好，那么原理是什么呢？首先，如果目标模型是一个线性模型，那么用FGSM就可以了，因为此时loss对输入的导数是固定的，换言之，使得loss下降的方向是明确的，即使你多次迭代，扰动的方向也不会改变。而对于一个非线性模型，仅仅做一次迭代，方向是不一定完全正确的，这也是为什么FGSM的效果一般的原因了。

用画图软件画了一个很丑的图，但大致能够表达我的看法，黑圈是输入样本，假设样本只有两维，那么样本可以改变的就有八个方向，坐标系中显示了loss等高线,以及可以扰动的最大范围（因为是无穷范数，所以限制范围是一个方形，负半轴的范围没有画出来），黑圈每一次改变，都是以最优的方向改变，最后一次由于扰动超出了限制，所以直接截断，如果此时迭代次数没有用完，那么就在截断处继续迭代，直到迭代次数用完。

2.PGD的代码实现

 class PGD(nn.Module):
     def __init__(self,model):
         super().__init__()
         self.model=model#必须是pytorch的model
         self.device=torch.device("cuda" if (torch.cuda.is_available()) else "cpu")
     def generate(self,x,**params):
         self.parse_params(**params)
         labels=self.y

         adv_x=self.attack(x,labels)
         return adv_x
     def parse_params(self,eps=0.3,iter_eps=0.01,nb_iter=40,clip_min=0.0,clip_max=1.0,C=0.0,
                      y=None,ord=np.inf,rand_init=True,flag_target=False):
         self.eps=eps
         self.iter_eps=iter_eps
         self.nb_iter=nb_iter
         self.clip_min=clip_min
         self.clip_max=clip_max
         self.y=y
         self.ord=ord
         self.rand_init=rand_init
         self.model.to(self.device)
         self.flag_target=flag_target
         self.C=C

     def sigle_step_attack(self,x,pertubation,labels):
         adv_x=x+pertubation
         # get the gradient of x
         adv_x=Variable(adv_x)
         adv_x.requires_grad = True
         loss_func=nn.CrossEntropyLoss()
         preds=self.model(adv_x)
         if self.flag_target:
             loss =-loss_func(preds,labels)
         else:
             loss=loss_func(preds,labels)
             # label_mask=torch_one_hot(labels)
             #
             # correct_logit=torch.mean(torch.sum(label_mask * preds,dim=1))
             # wrong_logit = torch.mean(torch.max((1 - label_mask) * preds, dim=1)[0])
             # loss=-F.relu(correct_logit-wrong_logit+self.C)

         self.model.zero_grad()
         loss.backward()
         grad=adv_x.grad.data
         #get the pertubation of an iter_eps
         pertubation=self.iter_eps*np.sign(grad)
         adv_x=adv_x.cpu().detach().numpy()+pertubation.cpu().numpy()
         x=x.cpu().detach().numpy()

         pertubation=np.clip(adv_x,self.clip_min,self.clip_max)-x
         pertubation=clip_pertubation(pertubation,self.ord,self.eps)

         return pertubation
     def attack(self,x,labels):
         labels = labels.to(self.device)
         print(self.rand_init)
         if self.rand_init:
             x_tmp=x+torch.Tensor(np.random.uniform(-self.eps, self.eps, x.shape)).type_as(x).cuda()
         else:
             x_tmp=x
         pertubation=torch.zeros(x.shape).type_as(x).to(self.device)
         for i in range(self.nb_iter):
             pertubation=self.sigle_step_attack(x_tmp,pertubation=pertubation,labels=labels)
             pertubation=torch.Tensor(pertubation).type_as(x).to(self.device)
         adv_x=x+pertubation
         adv_x=adv_x.cpu().detach().numpy()

         adv_x=np.clip(adv_x,self.clip_min,self.clip_max)

         return adv_x

PGD攻击的参数并不多，比较重要的就是下面这几个：

eps: maximum distortion of adversarial example compared to original input

eps_iter: step size for each attack iteration

nb_iter: Number of attack iterations.

我在上面代码中注释的这行代码是CW攻击的PGD形式，这个在防御论文https://arxiv.org/pdf/1706.06083.pdf中有体现，以后说到CW攻击再细说。

 # label_mask=torch_one_hot(labels)
 #
 # correct_logit=torch.mean(torch.sum(label_mask * preds,dim=1))
 # wrong_logit = torch.mean(torch.max((1 - label_mask) * preds, dim=1)[0])
 # loss=-F.relu(correct_logit-wrong_logit+self.C)

最后再提一点就是，在上面那篇防御论文中也提到了，PGD攻击是最强的一阶攻击，如果防御方法对这个攻击能够有很好的防御效果，那么其他攻击也不在话下了。

2019-03-29 20:43:40