洛谷1196【NOI2002】题解

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 3000030000 列，每列依次编号为 1, 2, …,300001,2,…,30000 。之后，他把自己的战舰也依次编号为 1, 2, …, 300001,2,…,30000 ，让第 ii 号战舰处于第 ii 列 (i = 1, 2, …, 30000)(i=1,2,…,30000) ，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 M_{i,j}Mi,j​ ，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令： C_{i,j}Ci,j​ 。该指令意思是，询问电脑，杨威利的第 ii 号战舰与第 jj 号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页……

输入输出格式

输入格式：

第一行有一个整数 T(1 \le T \le 500,000)T(1≤T≤500,000) ，表示总共有 TT 条指令。

以下有 TT 行，每行有一条指令。指令有两种格式：

1. M_{i,j}Mi,j​ ： ii 和 jj 是两个整数 (1 \le i,j \le 30000)(1≤i,j≤30000) ，表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第 ii 号战舰与第 jj 号战舰不在同一列。

2. C_{i,j}Ci,j​ ： ii 和 jj 是两个整数 (1 \le i,j \le 30000)(1≤i,j≤30000) ，表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式：

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 ii 号战舰与第 jj 号战舰之间布置的战舰数目。如果第 ii 号战舰与第 jj 号战舰当前不在同一列上，则输出 -1−1 。

输入输出样例

输入样例#1： 复制

4
M 2 3
C 1 2
M 2 4
C 4 2

输出样例#1： 复制

-1
1

说明

【样例说明】

战舰位置图：表格中阿拉伯数字表示战舰编号

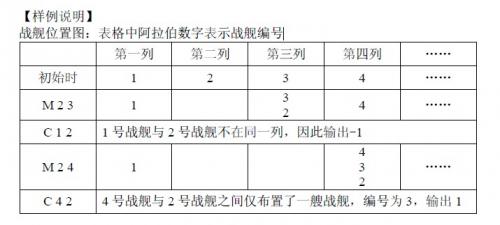
思路：根据这题对祖先更改的要求，很容易想到使用路径压缩的并查集。并且，对于要求C，我们的第一反映就是用前缀和处理。但是，如何在M操作后更新前缀和，是个问题。对于I队而言，队首元素为我代码中的X1，而X1的前缀和为0.因此，将X1的父亲接到Y1上后，利用路径压缩的回溯过程，把前缀和更新。这是此题对于并查集使用的最大特点：利用并查集回溯。

张贴代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int bcj[],len[],dis[];//len[i]表示第i队的长度
int T,x,y;
char k;
int czk(int i)
{
    if(bcj[i]==i)return i;
    else
    {
         int c=czk(bcj[i]);
         dis[i]+=dis[bcj[i]];//更新前缀和
         return bcj[i]=c;
    }
}
int main()
{
    for(int i=;i<=;i++)
    {
        bcj[i]=i;
        len[i]=;
        dis[i]=;
    }
    cin>>T;
    while(T--)
    {
        cin>>k;
        if(k=='M')
        {
            cin>>x>>y;
            int x1=czk(x);
            int y1=czk(y);
            dis[x1]+=len[y1];
            bcj[x1]=y1;
            len[y1]+=len[x1];
            len[x1]=;
        }
        else
        {
            cin>>x>>y;
            int x1=czk(x);
            int y1=czk(y);
            if(x1!=y1)cout<<"-1"<<endl;
            else cout<<abs(dis[x]-dis[y])-<<endl;
        }
    }
    return ;
}