【数据结构】【图文】【oj习题】 图的拓扑排序（邻接表）

拓扑排序：

按照有向图给出的次序关系，将图中顶点排成一个线性序列，对于有向图中没有限定次序关系的顶点，则可以人为加上任意的次序关系，由此所得顶点的线性序列称之为拓扑有序序列。显然对于有回路的有向图得不到拓扑有序序列，因为有回路的话，顶点的先后次序就不确定了。

例如：例如，下图，我们可以人为限定次序：A B C D 或 A C B D



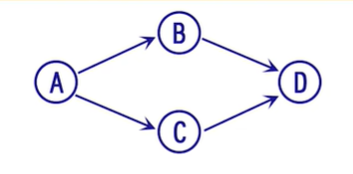
解释：该输出顺序特点就是后面的顶点输出必然后于该顶点的前驱顶点

算法：

1. 从有向图中选取一个没有前驱（没有在它之前活动）的顶点，输出之；
2. 从有向图中删去此顶点以及所有以它为尾的弧；
3. 重复上述两步，直至图空，或者图不空但找不到无前驱的顶点为止。
4. 没有被打印输出的顶点构成回路了。

那么、如何找到一个没有前驱的顶点呢？

通过解释看出，没有前驱的顶点的入度为零。我们每次重复第一个操作就是找到图中入度为零的点并且输出。

当然问题来了，如果图中有多个入度为零的顶点，如何判断谁先输出。或者怎么依次输出它们？

答：这里可以利用栈（队列），暂时将其入栈（入队），每次输出栈顶（队头）元素。因为每次都是输出的入度为零的节点，不同的存储方式可能造成输出顺序的不同，但是他们都遵循拓扑排序。都是拓扑排序的一种情况。

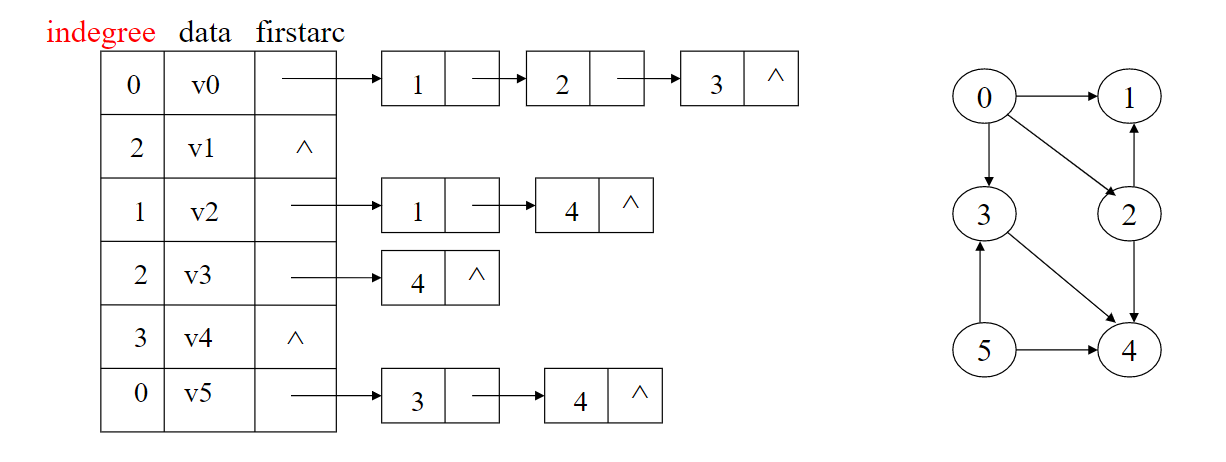
注意：

• ingress[]：用来存每个顶点的入度
• 图的存储结构：邻接表（不懂可以看我的上一篇随笔）

获取各顶点入度的函数：

void FindID(AdjList G, int indegree[MAX_VERTEX_NUM]){
	int i;
	ArcNode *p;
	for(i=0;i<G.vexnum;i++)			/*--初始化度数组----*/
		indegree[i]=0;
	for(i=0;i<G.vexnum;i++){
		p=G.vertexes[i].firstarc;		//找邻接点
		while(p!=NULL){
			indegree[p->adjvex]++;
			p=p->nextarc;
		}
	}
}

入栈方法输出拓扑排序

bool TopologicalSort(ALGraph G)
{

    SeqStack *s;
    s = (SeqStack*)malloc(sizeof(SeqStack));
    InitStack(s);				/*---初始化栈---*/
    int count,indegree[G.vexnum];		/*--count:用来计数---*/
    ArcNode *p;
    FindIndegree(G, indegree);			/*---获取各顶点入度的函数---*/
    int j;
    for(j = 0;j<G.vexnum;j++)
    {
        if(indegree[j]==0)
            push(s,j);				/*--找到一个度为零的入栈----*/
    }

    count = 0;

    while(!IsEmpty(s))				/*---栈非空---*/
    {
        int i = 0;

        Pop(s,&i);				/*---度为零的出栈并输出---*/
        printf("%d ",i);

        count++;
       for( p = G.adjlist[i].firstarc;p;p = p->nextarc)
       {					/*---将出栈的顶点尾部的弧’删除‘（其实是将所尾部连接的顶点的度减一）---*/
           indegree[p->adjvex]--;
           if(!indegree[p->adjvex]) push(s,p->adjvex);

       }

    }
    if(count == G.vexnum)			/*---出栈顶点数目等于图的顶点数说明图中无回路，否则有回路---*/
    {
        return true;
    }
    return false;

}

入对方法输出拓扑排序

int TopoSort(AdjList G){
	Queue Q;							/*队列存储入度为0*/
	int indegree[MAX_VERTEX_NUM];					//存放每个顶点的入度值
	int i,count,k;							//count计数，然后和有向图中顶点总数比较
	ArcNode*p;
	FindID(G,indegree);
	InitStack(&S);								//初始化队列
	for(i=0;i<G.vexnum;i++)
		if（indegree[i]==0) EnterQueue(&Q,i);				//入队
	count=0;
	while(!StackEmpty(S)){
		DeleteQueue(&Q,&i);						//一个入度为0的点出队
		printf("%c",G.vertex[i].data);
		count++;
		p=G.vertexes[i].firstarc;
		while(p!=NULL){
			k=p->adjvex;
			indegree[k]--;
			if(indegree[k]==0) EnterQueue(&S,k);
			p=p->nextarc;
		}
	}
	if(count<G.vexnum) return(Error);					//有向图中有回路
	else return(Ok);
}

时间复杂度

如果AOV网络有n个顶点，e条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是O(n)。在正常情况下，每个顶点进一次栈，出一次栈，所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。

oj题目要求：（入栈）拓扑排序