「Python实用秘技03」导出项目的极简环境依赖

本文完整示例代码及文件已上传至我的Github仓库https://github.com/CNFeffery/PythonPracticalSkills

　　这是我的系列文章「Python实用秘技」的第3期，本系列立足于笔者日常工作中使用Python积累的心得体会，每一期为大家带来一个3分钟即可学会的简单小技巧。

　　作为系列第3期，我们即将学习的是：导出项目的极简环境依赖。

　　很多朋友都知道，利用pip也好，利用conda也好，我们可以使用pip freeze、conda export等语句来对当前的Python环境依赖进行导出备份，以方便在其他机器上还原环境。

　　但此类环境依赖导出方法的局限在于，它会将当前环境下所有已安装的库信息进行导出，使得导出的结果繁杂臃肿。

　　而如果我们只想针对某个Python项目工程，将其内部真正导入的库信息进行导出，就可以用到pipreqs这个工具，使用pip install pipreqs进行安装之后，就可以以命令行的形式使用它，基础使用语法为：

pipreqs 目标工程根路径名

　　譬如pipreqs ./就将当前路径视作目标工程的根目录进行导出，以一个示例工程为例（其中encoding参数用于设置导出文件的编码，--force用于设置允许覆盖已存在的同名文件），并与pip freeze的结果进行对比，可以看到，pipreqs导出的环境依赖非常之简洁，在很多情况下更适合用来还原Python项目的最小依赖信息：

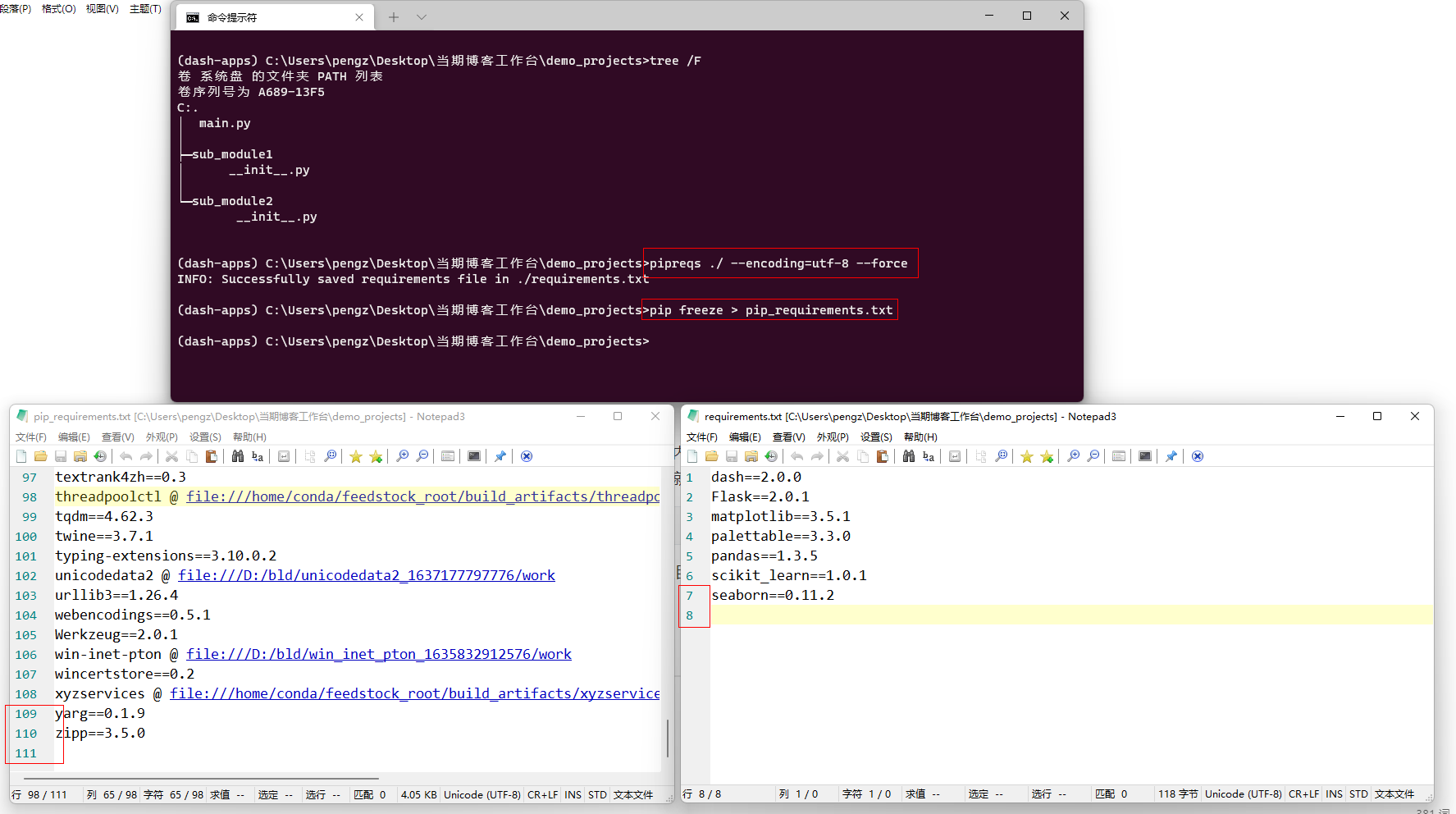
　　有了这个文件，在其他环境或机器上使用pip install requirements.txt命令就可以快速还原项目依赖，pipreqs还有一些实用的参数，你可以前往https://github.com/bndr/pipreqs#usage查看参数说明，快在你的项目中试试它吧~

---

　　本期分享结束，咱们下回见~