HDU2196 Computer【换根dp】

题目传送门

题意：

给定一个$N$个点的树，第$i$条边的长度是$A_i$，求每个点到其他所有点的最长距离。
数据范围：
$n ≤ 10000$，$A_i ≤ 10_9$

分析

首先，从随便哪个节点（$1$号节点（工具人））开始进行$dfs$，处理出所有点到$1$的距离$dis[i]$

然后，考虑$i$号节点的最远点。

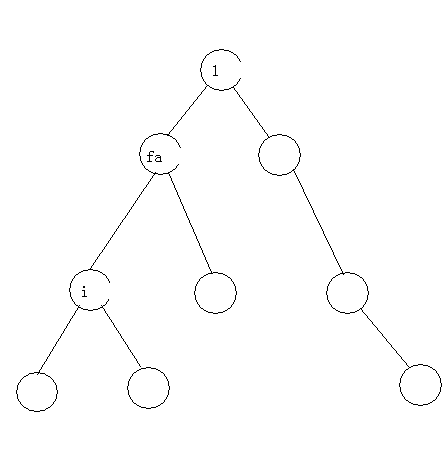
有两种情况：

一种是最远点在$i$的子树内，直接求就完事了（之前我们在以$1$为根的时候已经干过这件事情了）

另外一种就是经过了$i$和他父亲的那一条边，最远点在父亲的其它儿子中（或者是父亲的父亲的儿子中，当然，在把父亲看成根的情况下，就是父亲的其它儿子中，并且根据换根的做法，之前根已经被换到了父亲，答案是现成的）

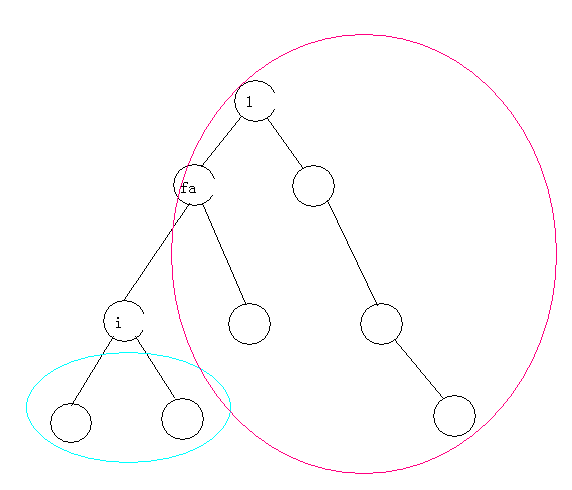
设离$i$最远的距离为$dist$，它父亲的子树中（以$1$为根节点形成的数）离它父亲最远的距离为$d1$，不在它父亲的子树中（通过了父亲<->爷爷这条边的）离它父亲最远的距离为$d2$，$i$和它父亲的的那一条边的权值为$w$

这种情况下，$dis=max(d1,d2)+w$

对于点$i$的答案，两种情况取$min$就可以啦。

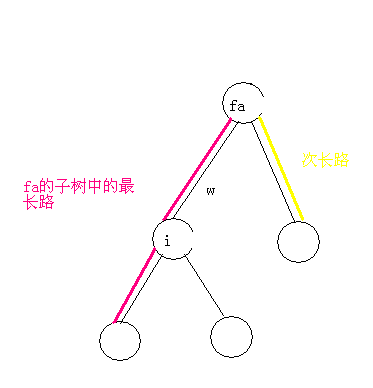
但是这样还存在一个问题，就是如果父亲的子树中离父亲最远的那条路经过了$i$，那么$dis$就不能从$d1$推过来，因为如果$max(d1,d2)=d1$，那就是$dis=d1+w$，而这肯定是不成立的，$d1$就包含了$w$和$i$到$i$子树中最远的路。

那么还需要维护一个次长路，当$i$在父亲到父亲子树中最远点的路径上时，要用次长路更新（这种情况下，这个次长路就是父亲的除$i$之外的最大儿子。

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 #include<queue>
 using namespace std;
 #define N 10005
 #define INF 0x3f3f3f3f
 #define ll long long
 int rd()
 {
     int f=,x=;char c=getchar();
     while(c<''||c>''){if(c=='-') f=-;c=getchar();}
     while(c>=''&&c<=''){x=(x<<)+(x<<)+(c^);c=getchar();}
     return f*x;
 }
 int n;
 int d1[N]/*距离i最长长度*/,d2[N]/*距离i次长长度*/;
 //d1[] d2[]都是子树i以内的
 int son[N]/*最长长度对应儿子编号*/;
 int anc[N]/*父亲方向最长长度(子树以外最长长度)*/;
 int ans[N];//答案
 struct node{
     int v,w;
 };
 vector<node>G[N];
 void dfs(int u,int f)
 {
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i].v,w=G[u][i].w;
         if(v==f) continue;
         dfs(v,u);
         if(d1[u]<d1[v]+w)
         {//从这个儿子能得到目前最长的长度
             d2[u]=d1[u];
             son[u]=v;
             d1[u]=d1[v]+w;
         }/*要写else 大儿子和二儿子要不一样*/
         else if(d2[u]<d1[v]+w)
             d2[u]=d1[v]+w;
         /*
         d2[v]不会被纳入答案中
         大儿子和二儿子要不一样
         无论如何都不会轮到d2[v]来做贡献
         如果d1[v]可以贡献 就贡献了 d2[v]也不会被用到
         如果d1[v]不能贡献 d2[v]就更不会被用到了
         */
     }
     ans[u]=d1[u];
 }
 void dfs2(int u,int f)
 {
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i].v,w=G[u][i].w;
         if(v==f) continue;
         if(v!=son[u])
             anc[v]=max(anc[u]+w,d1[u]+w);
         else anc[v]=max(anc[u]+w,d2[u]+w);
         ans[v]=max(ans[v],anc[v]);
         dfs2(v,u);
     }
 }
 int main()
 {
     while(scanf("%d",&n)!=EOF)
     {
         for(int i=;i<=n;i++)
         {
             int v=rd(),w=rd();
             node t;t.v=v,t.w=w;
             G[i].push_back(t);
             t.v=i;
             G[v].push_back(t);
             d1[i]=d2[i]=son[i]=anc[i]=ans[i]=;
         }
         d1[]=d2[]=son[]=anc[]=ans[]=;
         dfs(,);
         dfs2(,);
         for(int i=;i<=n;i++)
         {
             printf("%d\n",ans[i]);
             G[i].clear();
         }
     }
     return ;
 }

Code