损失函数 - Andrew Ng机器学习公开课笔记1.2
线性回归中提到最小二乘损失函数及其相关知识。对于这一部分知识不清楚的同学能够參考上一篇文章《线性回归、梯度下降》。
本篇文章主要解说使用最小二乘法法构建损失函数和最小化损失函数的方法。
最小二乘法构建损失函数
最小二乘法也一种优化方法,用于求得目标函数的最优值。简单的说就是:让我们的预測值与真实值总的拟合误差(即总残差)达到最小。
在线性回归中使用最小二乘法构建了损失函数:
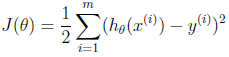
上一篇文章《线性回归、梯度下降》中提到求解使损失函数J(θ)取最小的θ值有两种方法:梯度下降(gradient descent)和正则方程(The normal equations)。以下主要讲一下正则方程。梯度下降方法最小化损失函数參考文章《线性回归、梯度下降》
正则方程
将训练特征表示为X矩阵,结果表示成y向量,仍然是线性回归模型。损失函数不变。那么θ能够直接由以下公式得出:

推导过程涉及线性代数方面的知识,这里不再具体展开线性代数知识。
设m为训练样本数;x为样本中的自变量,即二手房价格预測中的房屋面积和我是数目。x为n维向量;向量y为训练数据中的房屋价格。y为m维向量。那么训练数据能够用矩阵表示为:

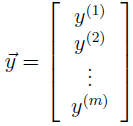
由于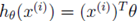 ,所以
,所以 就能够表示为:
就能够表示为:

损失函数就转化为:
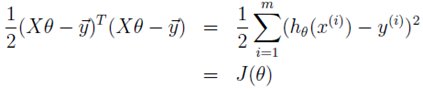
线性代数中有两个公式:
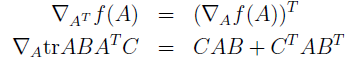
当中符号 表示一个m*n的矩阵。这个矩阵的第(i,j)个元素为
表示一个m*n的矩阵。这个矩阵的第(i,j)个元素为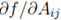 。
。
上面两个公式合起来能够表示为:

根据这这个公式对损失函数J(θ)推导:

为了最小化J(θ)。又由于J(θ)由最小二乘法得到,J(θ)的取值大于等于0。即最小值为0。
所以,我们使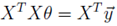 ,从而得到θ取值:
,从而得到θ取值:
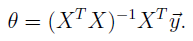
损失函数 - Andrew Ng机器学习公开课笔记1.2的更多相关文章
- Andrew Ng机器学习公开课笔记 -- 支持向量机
网易公开课,第6,7,8课 notes,http://cs229.stanford.edu/notes/cs229-notes3.pdf SVM-支持向量机算法概述, 这篇讲的挺好,可以参考 先继 ...
- Andrew Ng机器学习公开课笔记–Principal Components Analysis (PCA)
网易公开课,第14, 15课 notes,10 之前谈到的factor analysis,用EM算法找到潜在的因子变量,以达到降维的目的 这里介绍的是另外一种降维的方法,Principal Compo ...
- Andrew Ng机器学习公开课笔记 -- 学习理论
网易公开课,第9,10课 notes,http://cs229.stanford.edu/notes/cs229-notes4.pdf 这章要讨论的问题是,如何去评价和选择学习算法 Bias/va ...
- Andrew Ng机器学习公开课笔记 -- Regularization and Model Selection
网易公开课,第10,11课 notes,http://cs229.stanford.edu/notes/cs229-notes5.pdf Model Selection 首先需要解决的问题是,模型 ...
- Andrew Ng机器学习公开课笔记–Reinforcement Learning and Control
网易公开课,第16课 notes,12 前面的supervised learning,对于一个指定的x可以明确告诉你,正确的y是什么 但某些sequential decision making问题,比 ...
- Andrew Ng机器学习公开课笔记 – Factor Analysis
网易公开课,第13,14课 notes,9 本质上因子分析是一种降维算法 参考,http://www.douban.com/note/225942377/,浅谈主成分分析和因子分析 把大量的原始变量, ...
- Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降
网易公开课,监督学习应用.梯度下降 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 线性回归(Linear Regression) 先看个 ...
- Andrew Ng机器学习公开课笔记 -- Logistic Regression
网易公开课,第3,4课 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 前面讨论了线性回归问题, 符合高斯分布,使用最小二乘来作为损失函数 ...
- Andrew Ng机器学习公开课笔记–Independent Components Analysis
网易公开课,第15课 notes,11 参考, PCA本质是旋转找到新的基(basis),即坐标轴,并且新的基的维数大大降低 ICA也是找到新的基,但是目的是完全不一样的,而且ICA是不会降维的 对于 ...
随机推荐
- sql-server 2005数据库文件恢复(检測到基于一致性的逻辑 I/O 错误)
今天sql-server数据库突然报错: SQL Server 检測到基于一致性的逻辑 I/O 错误 校验和不对(应为: 0x7c781313,但实际为: 0x67a313c9). 在文件 'C:\P ...
- hdu1078 FatMouse and Cheese(记忆化搜索)
转载请注明出处:http://blog.csdn.net/u012860063 题目链接:pid=1078" target="_blank">http://acm. ...
- tomcat 分别在window 和 Linux上配置SSL-安全问题
公司项目收尾后.通过压力測试后的安全測试.安全測试后中,对于网络传输中数据加密问题存在安全隐患. 须要配置SSL. 简介下SSL协议:SSL或者Secure Socket Layer,是一种同意web ...
- 深入解析开源项目之Universal-Image-Loader(二)内存---缓存篇
珍惜作者劳动成果,如需转载,请注明出处. http://blog.csdn.net/zhengzechuan91/article/details/50292871 Universal-Image-Lo ...
- 如何让hudson的两个job共用一个svn工作目录
作者:朱金灿 来源:http://blog.csdn.net/clever101 现在我的需求是这样的:一个软件需要编译完全版本和基础版本,完全版本的基础功能较多,基础版本只包含了基础功能.有时只需要 ...
- 修改url中某个参数
function changeURLArg(url,arg,arg_val){ var pattern=arg+'=([^&]*)'; var replaceText=arg+'='+arg_ ...
- 【2017 Multi-University Training Contest - Team 2】Maximum Sequence
[Link]:http://acm.hdu.edu.cn/showproblem.php?pid=6047 [Description] 给你一个数列a和一个数列b; 只告诉你a的前n项各是什么; 然后 ...
- ReactJs 入门DEMO(转自别人)
附件是分享的一些他人的ReactJs入门DEMO,以前版本使用的是JSXTransformer.js,新版的用browser.min.js替代了. DEMO 下载地址:http://files.cnb ...
- C#解析HTML源码
刚做了一个小任务,需要抓取其他网站的部分数据,这里就顺便介绍使用Winista.Text.HtmlParser这个类库如何解析HTML并抓取部分数据 1.获取指定网站的页面源码 string url ...
- 2.2 Consumer API官网剖析(博主推荐)
不多说,直接上干货! 一切来源于官网 http://kafka.apache.org/documentation/ 2.2 Consumer API 2.2.消费者API 随着0..0版本,我们已经增 ...
