2021-02-26:一个数组arr是二叉树的中序遍历结果,每条边的开销是父节点和子节点的乘积,总开销是所有边的开销之和。请问最小总开销是多少?
2021-02-26:一个数组arr是二叉树的中序遍历结果,每条边的开销是父节点和子节点的乘积,总开销是所有边的开销之和。请问最小总开销是多少?
链接:https://www.nowcoder.com/questionTerminal/0d939e874a004f449a370aca1346dd5c
来源:牛客网
小团有一个由N个节点组成的二叉树,每个节点有一个权值。定义二叉树每条边的开销为其两端节点权值的乘积,二叉树的总开销即每条边的开销之和。小团按照二叉树的中序遍历依次记录下每个节点的权值,即他记录下了N个数,第i个数表示位于中序遍历第i个位置的节点的权值。之后由于某种原因,小团遗忘了二叉树的具体结构。在所有可能的二叉树中,总开销最小的二叉树被称为最优二叉树。现在,小团请小美求出最优二叉树的总开销。
输入描述:
第一行输入一个整数N(1<=N<=300),表示二叉树的节点数。
第二行输入N个由空格隔开的整数,表示按中序遍历记录下的各个节点的权值,所有权值均为不超过1000的正整数。
输出描述:
输出一个整数,表示最优二叉树的总开销。
福哥答案2021-02-26:
自然智慧即可。
1.递归。有代码。
2.记忆化搜索。有代码。
代码用golang编写,代码如下:
package main
import "fmt"
const MAX = int(^uint(0) >> 1)
//https://www.nowcoder.com/questionTerminal/0d939e874a004f449a370aca1346dd5c
func main() {
arr := []int{7, 6, 5, 1, 3}
ret := f1(arr)
fmt.Println("1.递归:", ret)
ret = f2(arr)
fmt.Println("2.记忆化搜索:", ret)
}
func f1(arr []int) int {
arrLen := len(arr)
if arrLen <= 1 {
return 0
}
return process1(arr, -1, 0, arrLen-1)
}
func process1(arr []int, cur int, L int, R int) int {
length := R - L + 1
if length == 0 {
return 0
}
ans := MAX
for i := L; i <= R; i++ {
temp := 0
if cur >= 0 {
temp = arr[cur] * arr[i]
}
ans = getMin(temp+process1(arr, i, L, i-1)+process1(arr, i, i+1, R), ans)
}
return ans
}
func f2(arr []int) int {
arrLen := len(arr)
if arrLen <= 1 {
return 0
}
dp := make([][][]int, arrLen+1)
for i := 0; i < arrLen+1; i++ {
dp[i] = make([][]int, arrLen)
for j := 0; j < arrLen; j++ {
dp[i][j] = make([]int, arrLen)
for k := 0; k < arrLen; k++ {
dp[i][j][k] = -1
}
}
}
ret := process2(arr, -1, 0, arrLen-1, dp)
//fmt.Println(dp)
return ret
}
func process2(arr []int, cur int, L int, R int, dp [][][]int) int {
length := R - L + 1
if length == 0 {
return 0
}
if dp[cur+1][L][R] != -1 {
//fmt.Println("记忆化", dp[cur+1][L][R])
return dp[cur+1][L][R]
}
ans := MAX
for i := L; i <= R; i++ {
temp := 0
if cur >= 0 {
temp = arr[cur] * arr[i]
}
ans = getMin(temp+process2(arr, i, L, i-1, dp)+process2(arr, i, i+1, R, dp), ans)
}
dp[cur+1][L][R] = ans
return ans
}
func getMin(a int, b int) int {
if a < b {
return a
} else {
return b
}
}
执行结果如下:
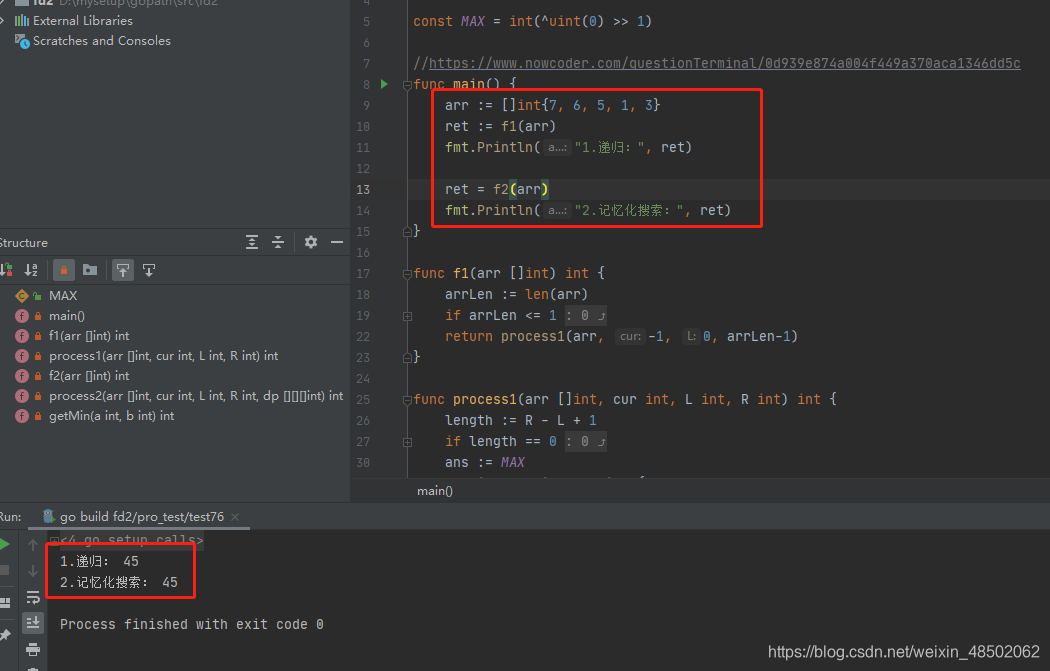
2021-02-26:一个数组arr是二叉树的中序遍历结果,每条边的开销是父节点和子节点的乘积,总开销是所有边的开销之和。请问最小总开销是多少?的更多相关文章
- 《剑指offer》第八题(重要!查找二叉树的中序遍历的下一个结点)
文件一:main.cpp // 面试题:二叉树的下一个结点 // 题目:给定一棵二叉树和其中的一个结点,如何找出中序遍历顺序的下一个结点? // 树中的结点除了有两个分别指向左右子结点的指针以外,还有 ...
- LeetCode 94:二叉树的中序遍历 Binary Tree Inorder Traversal
题目: 给定一个二叉树,返回它的中序 遍历. Given a binary tree, return the inorder traversal of its nodes' values. 示例: 输 ...
- [LeetCode] Binary Tree Inorder Traversal 二叉树的中序遍历
Given a binary tree, return the inorder traversal of its nodes' values. For example:Given binary tre ...
- LeetCode(94):二叉树的中序遍历
Medium! 题目描述: 给定一个二叉树,返回它的中序 遍历. 示例: 输入: [1,null,2,3] 1 \ 2 / 3 输出: [1,3,2] 进阶: 递归算法很简单,你可以通过迭代算法完成吗 ...
- 【LeetCode题解】94_二叉树的中序遍历
目录 [LeetCode题解]94_二叉树的中序遍历 描述 方法一:递归 Java 代码 Python代码 方法二:非递归 Java 代码 Python 代码 [LeetCode题解]94_二叉树的中 ...
- LeetCode 94. 二叉树的中序遍历(Binary Tree Inorder Traversal)
94. 二叉树的中序遍历 94. Binary Tree Inorder Traversal 题目描述 给定一个二叉树,返回它的 中序 遍历. LeetCode94. Binary Tree Inor ...
- Leetcode题目94.二叉树的中序遍历(中等)
题目描述: 给定一个二叉树,返回它的中序遍历. 示例: 输入: [1,null,2,3] 1 \ 2 / 3 输出: [1,3,2] 进阶: 递归算法很简单,你可以通过迭代算法完成吗? 思路解析: 1 ...
- leecode刷题(29)-- 二叉树的中序遍历
leecode刷题(29)-- 二叉树的中序遍历 二叉树的中序遍历 给定一个二叉树,返回它的中序 遍历. 示例: 输入: [1,null,2,3] 1 \ 2 / 3 输出: [1,3,2] 思路 跟 ...
- Java实现 LeetCode 94 二叉树的中序遍历
94. 二叉树的中序遍历 给定一个二叉树,返回它的中序 遍历. 示例: 输入: [1,null,2,3] 1 2 / 3 输出: [1,3,2] 进阶: 递归算法很简单,你可以通过迭代算法完成吗? / ...
- 【LeetCode】94. 二叉树的中序遍历
94. 二叉树的中序遍历 知识点:二叉树:递归:Morris遍历 题目描述 给定一个二叉树的根节点 root ,返回它的 中序 遍历. 示例 输入:root = [1,null,2,3] 输出:[1, ...
随机推荐
- TP5.1模板循环标签
第一种volist name=assign中的变量名 id=数组中的key offset=开始循环的位置 length=步长 {volist name='list' id='vo' offset='0 ...
- TProtocolException: Required field 'type' is unset! Struct:TPrimitiveTypeEntry(type:null)
org.apache.thrift.protocol.TProtocolException: Required field 'type' is unset! Struct:TPrimitiveType ...
- 文件上传 upload-labs Pass-17 二次渲染
Pass-17 审计源码 $is_upload = false; $msg = null; if (isset($_POST['submit'])){ // 获得上传文件的基本信息,文件名,类型,大小 ...
- 说来惭愧,关于Session的某块知识的学习,感觉涨了知识
Session的查漏补缺 今天在写界面的时候,想要利用servlet和jsp页面实现界面的跳转,之前实现这些内容的时候,我是没有用到session来实现这个功能的. 直到今天,想要将第一个界面的数据隔 ...
- [WinUI 3] 如何利用D3D11在SwapChainPanel控件上绘制OpenGL(Uwp通用)
预览 技术实现 看过我上篇在 WPF 中实现 OpenGL 与 D3D 渲染的同学应该知道,我是依靠 WGL 中 WGL_NV_DX_interop 扩展与 D3D Surface 关联并在使用该 S ...
- 基于 ByteHouse 构建实时数仓实践
更多技术交流.求职机会,欢迎关注字节跳动数据平台微信公众号,回复[1]进入官方交流群 随着数据的应用场景越来越丰富,企业对数据价值反馈到业务中的时效性要求也越来越高,很早就有人提出过一个概念: 数据的 ...
- 基于Admin.NET框架的前端的一些改进和代码生成处理(1)
Admin.NET 是一套基于Furion/.NET 6实现的通用管理平台,模块插件式开发,框架包含了常规的权限管理.字典等管理模块,以及一些Vue3的Demo案例,框架前后端分离.后端基于基于Fur ...
- git的Rebase和Merge之间的区别
有人会说Merge更好,因为它保留了最完整的工作历史.其他人则认为,Rebase变得更整洁,这使审阅者的生活更轻松,更高效.本文将解释合并和重新设置之间的区别是什么,使用它们之一有什么好处. 从根本上 ...
- WebDriver API及对象识别技术
html页面的iframe的切换: iframe框架在html页面:实际就是多个html页面的相互嵌套:如果存在多个,则操作对象一直停留在主文档页面: 如果需要操作子文档页面则需要实现ifram ...
- Centos9网卡配置
Centos9 网卡配置文件已修改,如下 [root@bogon ~]# cat /etc/NetworkManager/system-connections/ens18.nmconnection [ ...
