线性dp：LeetCode516 .最长回文子序列

LeetCode516 .最长回文子序列

题目叙述：

力扣题目链接(opens new window)

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

• 1 <= s.length <= 1000
• s 仅由小写英文字母组成

动态规划思路

• 我们在上文中已经介绍了回文子串，那么我们可以沿用回文子串的思想解决这道题，但是我们首先得明确回文子串和回文子序列的区别

• LeetCode647.回文子串求的是回文子串，而本题要求的是回文子序列， 要搞清楚这两者之间的区别。

• 回文子串是要连续的，回文子序列可不是连续的！ 回文子串，回文子序列都是动态规划经典题目。

• 回文子串，可以做这两题：

  • 647.回文子串

  • 5.最长回文子串

思路其实是差不多的，但本题要比求回文子串简单一点，因为情况少了一点。

动规五部曲分析如下：

1.确定状态变量及其含义

• 我们设立dp数组，dp[i]] [j] 表示s字符串在[i，j]范围内最长回文子序列的长度。（j>=i）
• 那么我们确立了状态变量dp[i][j]，那么我们就要开始处理递推公式和如何初始化了

2.确定递推公式

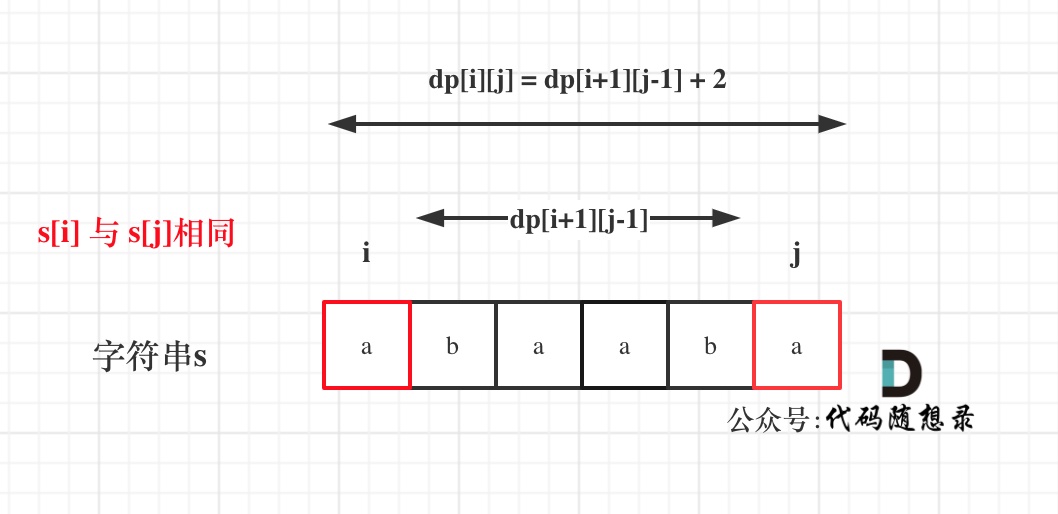
• 在这里，我们最重要的就是判断s[i],s[j]之间的关系
  • s[i]==s[j] 此时，dp[i][j]=dp[i+1][j-1]+2
• 为什么是+2呢？因为本题是最长回文子序列，当s[i]==s[j]时，[i,j]范围内至少有dp[i+1][j-1]+2这个大小的最长回文子序列，+2就是加上s[i],s[j]这两个字符。

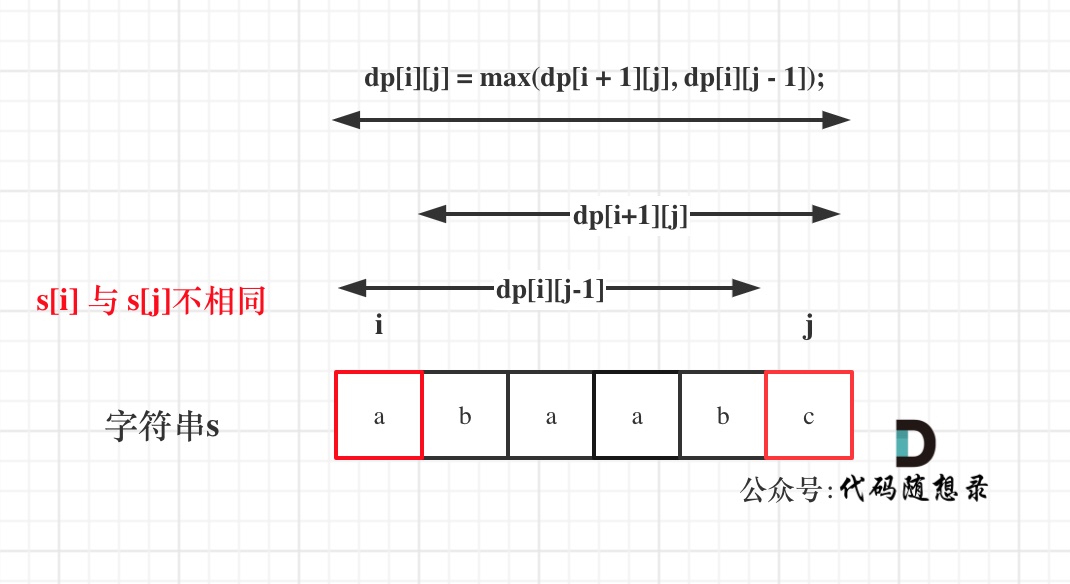
• 如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1] [j]。

加入s[i]的回文子序列长度为dp[i] [j - 1]。

那么dp [i] [j]一定是取最大的，即：dp [i] [j] = max(dp [i + 1] [j], dp[i] [j - 1]);

3.如何初始化dp数组

• 首先，我们得处理特殊情况，当i==j的时候，这个时候在[i,j]范围内只有一个字符，使用dp[i][j]=dp[i+1][j-1]+2 会导致当前处理的子串的左边界大于右边界，此时我们就得特殊处理一下，当处理的子串只有一个字符时，i==j，并且dp[i][j]显然等于1，因为单个字符也是回文子序列，并且这个回文子序列的长度是1。

vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

4. 确定遍历顺序

从递归公式中，可以看出，dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，如图：

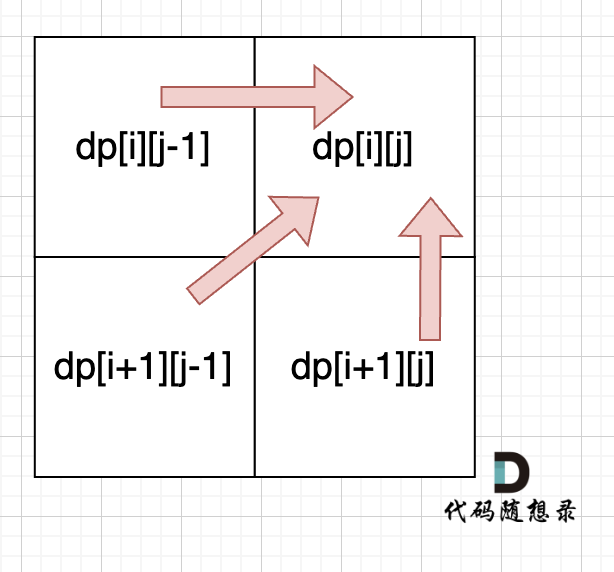
• 所以说我们想要得到dp[i][j] ，必须从左下方开始，向着右上方的方向进行递推。
• 所以说遍历顺序就是从下到上，从左到右

        //开始对dp数组进行从下到上，从左到右进行赋值。
        for(int i=s.size()-1;i>=0;i--){
            for(int j=i+1;j<s.size();j++){
                if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2;
                else dp[i][j]=max(dp[i][j-1],dp[i+1][j]);
            }
        }

5.举例打印dp数组

输入s:"cbbd" 为例，dp数组状态如图：

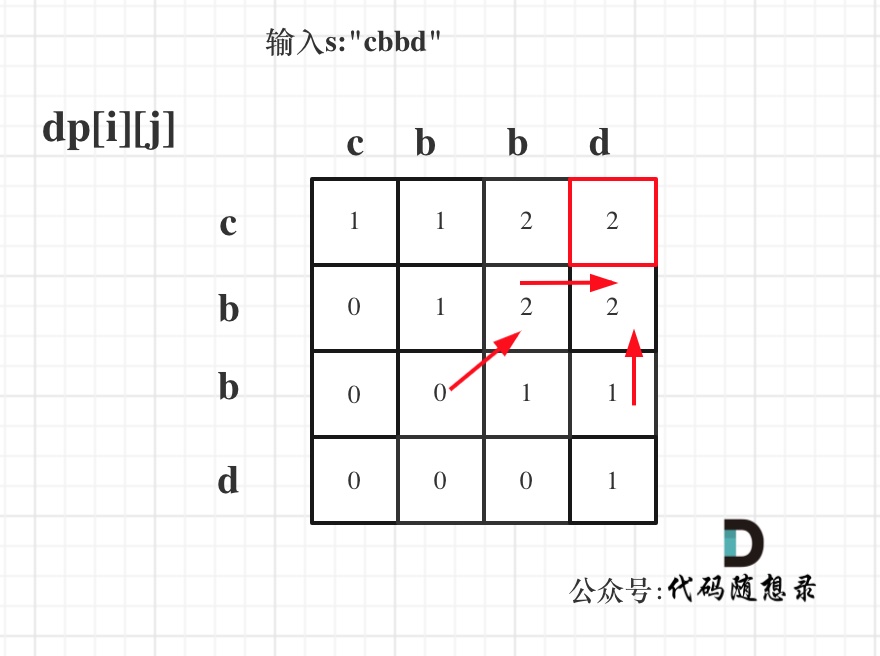
红色框即：dp[0][s.size() - 1]; 为最终结果。

最终代码：

//最长回文子序列
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        //创建二维的dp数组
        vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
        //初始化dp数组，首先要将i和j相等的时候，也就是只有一个字符的子序列，它的dp值赋值为1
        for(int i=0;i<s.size();i++) dp[i][i]=1;
        //开始对dp数组进行从下到上，从左到右进行赋值。
        for(int i=s.size()-1;i>=0;i--){
            for(int j=i+1;j<s.size();j++){
                if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2;
                else dp[i][j]=max(dp[i][j-1],dp[i+1][j]);
            }
        }
        //最后，从0-s.size()-1这个范围的最长回文子序列的长度就是我们需要的答案。
        return dp[0][s.size()-1];
    }
};

注明

• 本文中引用了作者代码随想录的部分图片和原文，若想深入了解，可以去原作者的文章阅读
• 代码随想录